Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 202019 by MATHEMATICSAM last updated on 18/Dec/23

If α and β are the roots of the ax^2 + 2bx + c = 0 and α + δ and β + δ are the roots of Ax^2 + 2Bx + C = 0 for some constant δ then prove that ((b^2 − ac)/a^2 ) = ((B^2 − AC)/A^2 ) .

$$\mathrm{If}\:\alpha\:\mathrm{and}\:\beta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\: \\ $$$${ax}^{\mathrm{2}} \:+\:\mathrm{2}{bx}\:+\:{c}\:=\:\mathrm{0}\:\mathrm{and}\:\alpha\:+\:\delta\:\mathrm{and}\:\beta\:+\:\delta\:\mathrm{are} \\ $$$$\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:{Ax}^{\mathrm{2}} \:+\:\mathrm{2}{Bx}\:+\:{C}\:=\:\mathrm{0}\:\mathrm{for}\:\mathrm{some}\: \\ $$$$\mathrm{constant}\:\delta\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\frac{{b}^{\mathrm{2}} \:−\:{ac}}{{a}^{\mathrm{2}} }\:=\:\frac{{B}^{\mathrm{2}} \:−\:{AC}}{{A}^{\mathrm{2}} }\:. \\ $$

Answered by esmaeil last updated on 18/Dec/23

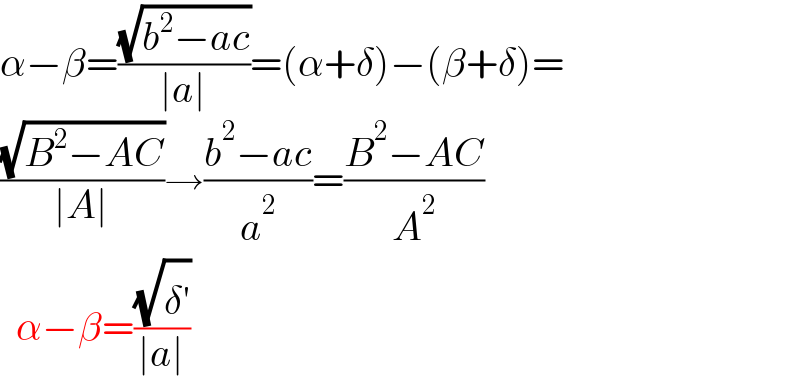
α−β=((√(b^2 −ac))/(∣a∣))=(α+δ)−(β+δ)= ((√(B^2 −AC))/(∣A∣))→((b^2 −ac)/a^2 )=((B^2 −AC)/A^2 ) α−β=((√δ^′ )/(∣a∣))

$$\alpha−\beta=\frac{\sqrt{{b}^{\mathrm{2}} −{ac}}}{\mid{a}\mid}=\left(\alpha+\delta\right)−\left(\beta+\delta\right)= \\ $$$$\frac{\sqrt{{B}^{\mathrm{2}} −{AC}}}{\mid{A}\mid}\rightarrow\frac{{b}^{\mathrm{2}} −{ac}}{{a}^{\mathrm{2}} }=\frac{{B}^{\mathrm{2}} −{AC}}{{A}^{\mathrm{2}} } \\ $$$$\:\:\alpha−\beta=\frac{\sqrt{\delta^{'} }}{\mid{a}\mid} \\ $$

Commented by MM42 last updated on 18/Dec/23

⋛

$$\:\cancel{\lesseqgtr} \\ $$

Answered by Rasheed.Sindhi last updated on 19/Dec/23

Another way •α & β are the roots of ax^2 + 2bx + c = 0 α+β=−((2b)/a) , αβ=(c/a) •If the roots are α+δ & β+δ (δ is fixed constant) The equation will be: (α+δ)+(β+δ)=α+β+2δ=−((2b)/a)+2δ=−((2B)/A) ⇒(B/A)=((−2b+2aδ)/(−2a)) (α+δ).(β+δ)=αβ+δ^2 +(α+β)δ=(c/a)−((2bδ)/a)+δ^2 =(C/A) ⇒(C/A)=((c−2bδ+aδ^2 )/a) ((B^2 − AC)/A^2 )=((B/A))^2 −(C/A)=(((−2b+2aδ)/(−2a)))^2 −((c−2bδ+aδ^2 )/a) =((4b^2 +4a^2 δ^2 −8abδ)/(4a^2 ))−((c−2bδ+aδ^2 )/a) =((4b^2 +4a^2 δ^2 −8abδ−4ac+8abδ−4a^2 δ^2 )/(4a^2 )) =((4b^2 −4ac)/(4a^2 ))=((b^2 −ac)/a^2 ) QED

$${Another}\:{way} \\ $$$$\bullet\alpha\:\&\:\beta\:{are}\:{the}\:{roots}\:{of}\:{ax}^{\mathrm{2}} \:+\:\mathrm{2}{bx}\:+\:{c}\:=\:\mathrm{0} \\ $$$$\:\:\:\alpha+\beta=−\frac{\mathrm{2}{b}}{{a}}\:,\:\alpha\beta=\frac{{c}}{{a}} \\ $$$$\bullet\mathcal{I}{f}\:{the}\:{roots}\:{are}\:\alpha+\delta\:\&\:\beta+\delta\:\left(\delta\:{is}\:{fixed}\:{constant}\right) \\ $$$$\:\:\:\mathcal{T}{he}\:{equation}\:{will}\:{be}: \\ $$$$\:\:\:\left(\alpha+\delta\right)+\left(\beta+\delta\right)=\alpha+\beta+\mathrm{2}\delta=−\frac{\mathrm{2}{b}}{{a}}+\mathrm{2}\delta=−\frac{\mathrm{2}{B}}{{A}} \\ $$$$\Rightarrow\frac{{B}}{{A}}=\frac{−\mathrm{2}{b}+\mathrm{2}{a}\delta}{−\mathrm{2}{a}} \\ $$$$\:\:\:\left(\alpha+\delta\right).\left(\beta+\delta\right)=\alpha\beta+\delta^{\mathrm{2}} +\left(\alpha+\beta\right)\delta=\frac{{c}}{{a}}−\frac{\mathrm{2}{b}\delta}{{a}}+\delta^{\mathrm{2}} =\frac{{C}}{{A}} \\ $$$$\Rightarrow\frac{{C}}{{A}}=\frac{{c}−\mathrm{2}{b}\delta+{a}\delta^{\mathrm{2}} }{{a}} \\ $$$$\:\frac{{B}^{\mathrm{2}} \:−\:{AC}}{{A}^{\mathrm{2}} }=\left(\frac{{B}}{{A}}\right)^{\mathrm{2}} −\frac{{C}}{{A}}=\left(\frac{−\mathrm{2}{b}+\mathrm{2}{a}\delta}{−\mathrm{2}{a}}\right)^{\mathrm{2}} −\frac{{c}−\mathrm{2}{b}\delta+{a}\delta^{\mathrm{2}} }{{a}} \\ $$$$\:\:\:\:=\frac{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} \delta^{\mathrm{2}} −\mathrm{8}{ab}\delta}{\mathrm{4}{a}^{\mathrm{2}} }−\frac{{c}−\mathrm{2}{b}\delta+{a}\delta^{\mathrm{2}} }{{a}} \\ $$$$\:\:\:\:=\frac{\mathrm{4}{b}^{\mathrm{2}} +\cancel{\mathrm{4}{a}^{\mathrm{2}} \delta^{\mathrm{2}} }−\cancel{\mathrm{8}{ab}\delta}−\mathrm{4}{ac}+\cancel{\mathrm{8}{ab}\delta}−\cancel{\mathrm{4}{a}^{\mathrm{2}} \delta^{\mathrm{2}} }}{\mathrm{4}{a}^{\mathrm{2}} } \\ $$$$\:\:\:\:=\frac{\mathrm{4}{b}^{\mathrm{2}} −\mathrm{4}{ac}}{\mathrm{4}{a}^{\mathrm{2}} }=\frac{{b}^{\mathrm{2}} −{ac}}{{a}^{\mathrm{2}} } \\ $$$${QED} \\ $$

Answered by Rasheed.Sindhi last updated on 19/Dec/23

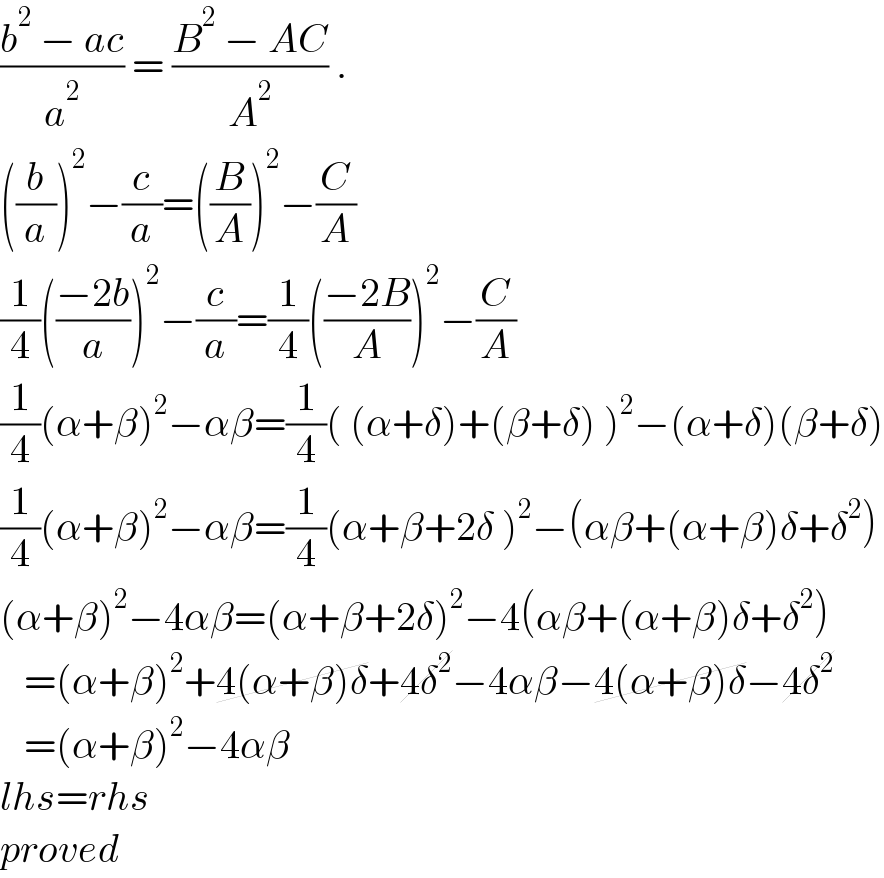
((b^2 − ac)/a^2 ) = ((B^2 − AC)/A^2 ) . ((b/a))^2 −(c/a)=((B/A))^2 −(C/A) (1/4)(((−2b)/a))^2 −(c/a)=(1/4)(((−2B)/A))^2 −(C/A) (1/4)(α+β)^2 −αβ=(1/4)( (α+δ)+(β+δ) )^2 −(α+δ)(β+δ) (1/4)(α+β)^2 −αβ=(1/4)(α+β+2δ )^2 −(αβ+(α+β)δ+δ^2 ) (α+β)^2 −4αβ=(α+β+2δ)^2 −4(αβ+(α+β)δ+δ^2 ) =(α+β)^2 +4(α+β)δ+4δ^2 −4αβ−4(α+β)δ−4δ^2 =(α+β)^2 −4αβ lhs=rhs proved

$$\frac{{b}^{\mathrm{2}} \:−\:{ac}}{{a}^{\mathrm{2}} }\:=\:\frac{{B}^{\mathrm{2}} \:−\:{AC}}{{A}^{\mathrm{2}} }\:. \\ $$$$\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} −\frac{{c}}{{a}}=\left(\frac{{B}}{{A}}\right)^{\mathrm{2}} −\frac{{C}}{{A}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{−\mathrm{2}{b}}{{a}}\right)^{\mathrm{2}} −\frac{{c}}{{a}}=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{−\mathrm{2}{B}}{{A}}\right)^{\mathrm{2}} −\frac{{C}}{{A}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left(\alpha+\beta\right)^{\mathrm{2}} −\alpha\beta=\frac{\mathrm{1}}{\mathrm{4}}\left(\:\left(\alpha+\delta\right)+\left(\beta+\delta\right)\:\right)^{\mathrm{2}} −\left(\alpha+\delta\right)\left(\beta+\delta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left(\alpha+\beta\right)^{\mathrm{2}} −\alpha\beta=\frac{\mathrm{1}}{\mathrm{4}}\left(\alpha+\beta+\mathrm{2}\delta\:\right)^{\mathrm{2}} −\left(\alpha\beta+\left(\alpha+\beta\right)\delta+\delta^{\mathrm{2}} \right) \\ $$$$\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{4}\alpha\beta=\left(\alpha+\beta+\mathrm{2}\delta\right)^{\mathrm{2}} −\mathrm{4}\left(\alpha\beta+\left(\alpha+\beta\right)\delta+\delta^{\mathrm{2}} \right) \\ $$$$\:\:\:=\left(\alpha+\beta\right)^{\mathrm{2}} +\cancel{\mathrm{4}\left(\alpha+\beta\right)\delta}+\cancel{\mathrm{4}\delta^{\mathrm{2}} }−\mathrm{4}\alpha\beta−\cancel{\mathrm{4}\left(\alpha+\beta\right)\delta}−\cancel{\mathrm{4}\delta^{\mathrm{2}} } \\ $$$$\:\:\:=\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{4}\alpha\beta \\ $$$${lhs}={rhs} \\ $$$${proved} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com