
Question Number 201966 by mnjuly1970 last updated on 17/Dec/23
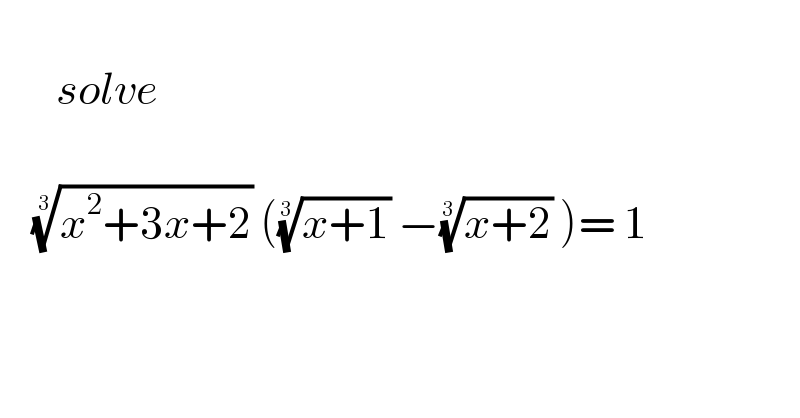
$$ \\ $$$$\:\:\:\:\:\:\:{solve}\: \\ $$$$\:\: \\ $$$$\:\:\:\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}}\:\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}\:−\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:\right)=\:\mathrm{1} \\ $$$$ \\ $$
Answered by ajfour last updated on 17/Dec/23
![let x+(3/2)=t ⇒ p=x+1=t−(1/2) q=x+2=t+(1/2) ⇒ −R= x^2 +3x+2=t^2 −(1/4) pq=−R (t^2 −(1/4))[−1−((3(pq)^(1/3) )/((t^2 −(1/4))^(1/3) ))]=1 −1−((3(pq)^(1/3) )/((t^2 −(1/4))^(1/3) ))= −(1/R) ((1/R)−1)^3 =((27(−R))/(−R)) ⇒ (1/R)−1=3 ⇒ R=(1/4) x^2 +3x+2=−(1/4) x^2 +3x+(9/4)=0 (x+(3/2))^2 =0 x= −(3/2)](Q201967.png)
$${let}\:\:{x}+\frac{\mathrm{3}}{\mathrm{2}}={t}\:\:\Rightarrow\:\:{p}={x}+\mathrm{1}={t}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${q}={x}+\mathrm{2}={t}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:−{R}=\:{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}={t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${pq}=−{R} \\ $$$$\left({t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)\left[−\mathrm{1}−\frac{\mathrm{3}\left({pq}\right)^{\mathrm{1}/\mathrm{3}} }{\left({t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{1}/\mathrm{3}} }\right]=\mathrm{1} \\ $$$$−\mathrm{1}−\frac{\mathrm{3}\left({pq}\right)^{\mathrm{1}/\mathrm{3}} }{\left({t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{1}/\mathrm{3}} }=\:\:−\frac{\mathrm{1}}{{R}} \\ $$$$\left(\frac{\mathrm{1}}{{R}}−\mathrm{1}\right)^{\mathrm{3}} =\frac{\mathrm{27}\left(−{R}\right)}{−{R}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{{R}}−\mathrm{1}=\mathrm{3}\:\:\Rightarrow\:\:{R}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}+\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 17/Dec/23
$$\:\:{thanks}\:{alot}\:{sir}\:{ajfor} \\ $$$$\:\: \\ $$
Answered by Frix last updated on 17/Dec/23
![(ab)^(1/3) (a^(1/3) −b^(1/3) )=1 a^(1/3) −b^(1/3) _(★) =(ab)^(−(1/3)) a−3(ab)^(1/3) (a^(1/3) −b^(1/3) _(★) )−b=(ab)^(−1) a−b−3=(1/(ab)) a=x+1∧b=x+2 x^2 +3x+(9/4)=0 x=−(3/2) [Only true if we stay ∈R ⇒ ((−r))^(1/3) =−(r)^(1/3) ]](Q201973.png)
$$\left({ab}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \left({a}^{\frac{\mathrm{1}}{\mathrm{3}}} −{b}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)=\mathrm{1} \\ $$$$\underset{\bigstar} {\underbrace{{a}^{\frac{\mathrm{1}}{\mathrm{3}}} −{b}^{\frac{\mathrm{1}}{\mathrm{3}}} }}=\left({ab}\right)^{−\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${a}−\mathrm{3}\left({ab}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\underset{\bigstar} {\underbrace{{a}^{\frac{\mathrm{1}}{\mathrm{3}}} −{b}^{\frac{\mathrm{1}}{\mathrm{3}}} }}\right)−{b}=\left({ab}\right)^{−\mathrm{1}} \\ $$$${a}−{b}−\mathrm{3}=\frac{\mathrm{1}}{{ab}} \\ $$$${a}={x}+\mathrm{1}\wedge{b}={x}+\mathrm{2} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}+\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{0} \\ $$$${x}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left[\mathrm{Only}\:\mathrm{true}\:\mathrm{if}\:\mathrm{we}\:\mathrm{stay}\:\in\mathbb{R}\:\Rightarrow\:\sqrt[{\mathrm{3}}]{−{r}}=−\sqrt[{\mathrm{3}}]{{r}}\right] \\ $$
Commented by Frix last updated on 17/Dec/23

$$...\mathrm{and}\:\mathrm{no}\:\mathrm{complex}\:\mathrm{solutions}. \\ $$
