
Question Number 21655 by Joel577 last updated on 30/Sep/17
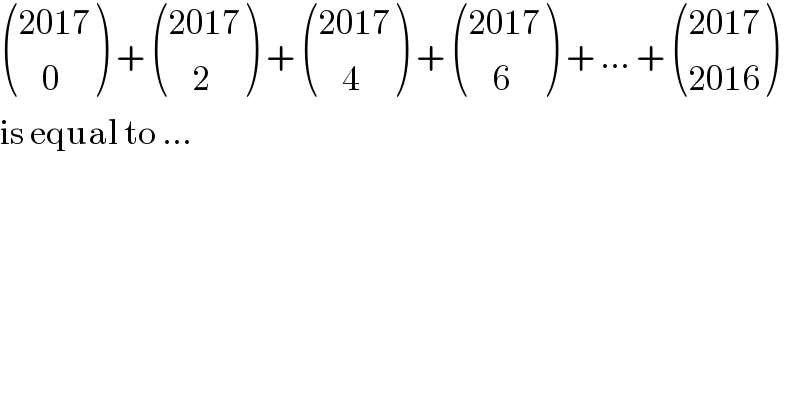
$$\begin{pmatrix}{\mathrm{2017}}\\{\:\:\:\:\mathrm{0}}\end{pmatrix}\:+\:\begin{pmatrix}{\mathrm{2017}}\\{\:\:\:\:\mathrm{2}}\end{pmatrix}\:+\:\begin{pmatrix}{\mathrm{2017}}\\{\:\:\:\:\mathrm{4}}\end{pmatrix}\:+\:\begin{pmatrix}{\mathrm{2017}}\\{\:\:\:\:\mathrm{6}}\end{pmatrix}\:+\:...\:+\:\begin{pmatrix}{\mathrm{2017}}\\{\mathrm{2016}}\end{pmatrix} \\ $$$$\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:... \\ $$
Answered by $@ty@m last updated on 30/Sep/17
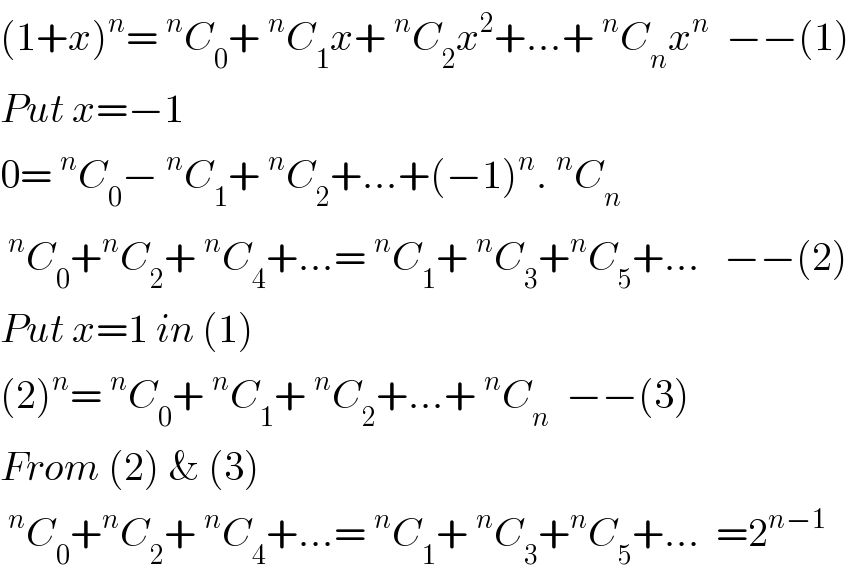
$$\left(\mathrm{1}+{x}\right)^{{n}} =\:^{{n}} {C}_{\mathrm{0}} +\:^{{n}} {C}_{\mathrm{1}} {x}+\:^{{n}} {C}_{\mathrm{2}} {x}^{\mathrm{2}} +...+\:^{{n}} {C}_{{n}} {x}^{{n}} \:\:−−\left(\mathrm{1}\right) \\ $$$${Put}\:{x}=−\mathrm{1} \\ $$$$\mathrm{0}=\:^{{n}} {C}_{\mathrm{0}} −\:^{{n}} {C}_{\mathrm{1}} +\:^{{n}} {C}_{\mathrm{2}} +...+\left(−\mathrm{1}\right)^{{n}} .\:^{{n}} {C}_{{n}} \\ $$$$\:^{{n}} {C}_{\mathrm{0}} +^{{n}} {C}_{\mathrm{2}} +\:^{{n}} {C}_{\mathrm{4}} +...=\:^{{n}} {C}_{\mathrm{1}} +\:^{{n}} {C}_{\mathrm{3}} +^{{n}} {C}_{\mathrm{5}} +...\:\:\:−−\left(\mathrm{2}\right) \\ $$$${Put}\:{x}=\mathrm{1}\:{in}\:\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{2}\right)^{{n}} =\:^{{n}} {C}_{\mathrm{0}} +\:^{{n}} {C}_{\mathrm{1}} +\:^{{n}} {C}_{\mathrm{2}} +...+\:^{{n}} {C}_{{n}} \:\:−−\left(\mathrm{3}\right) \\ $$$${From}\:\left(\mathrm{2}\right)\:\&\:\left(\mathrm{3}\right) \\ $$$$\:^{{n}} {C}_{\mathrm{0}} +^{{n}} {C}_{\mathrm{2}} +\:^{{n}} {C}_{\mathrm{4}} +...=\:^{{n}} {C}_{\mathrm{1}} +\:^{{n}} {C}_{\mathrm{3}} +^{{n}} {C}_{\mathrm{5}} +...\:\:=\mathrm{2}^{{n}−\mathrm{1}} \\ $$
Commented by Joel577 last updated on 30/Sep/17
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by $@ty@m last updated on 30/Sep/17
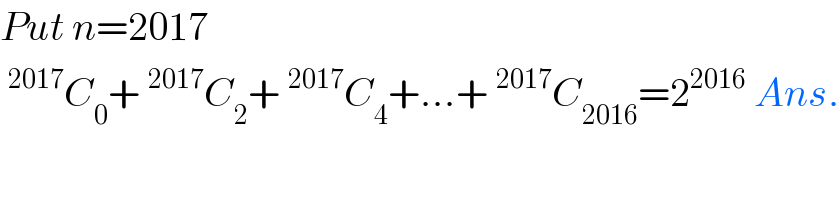
$${Put}\:{n}=\mathrm{2017} \\ $$$$\:^{\mathrm{2017}} {C}_{\mathrm{0}} +\:^{\mathrm{2017}} {C}_{\mathrm{2}} +\:^{\mathrm{2017}} {C}_{\mathrm{4}} +...+\:^{\mathrm{2017}} {C}_{\mathrm{2016}} =\mathrm{2}^{\mathrm{2016}} \:{Ans}. \\ $$
