Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 200961 by jabarsing last updated on 27/Nov/23

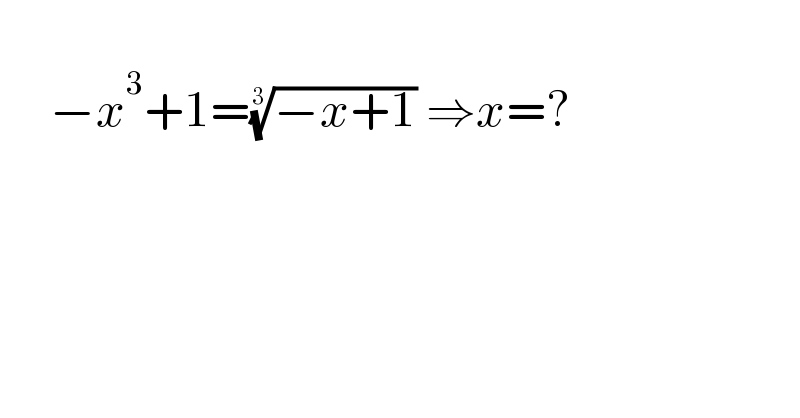
−x^3 +1=((−x+1))^(1/3) ⇒x=?

$$\: \\ $$$$\:\:\:\:\:−{x}^{\mathrm{3}} +\mathrm{1}=\sqrt[{\mathrm{3}}]{−{x}+\mathrm{1}}\:\Rightarrow{x}=? \\ $$$$ \\ $$

Answered by cortano12 last updated on 27/Nov/23

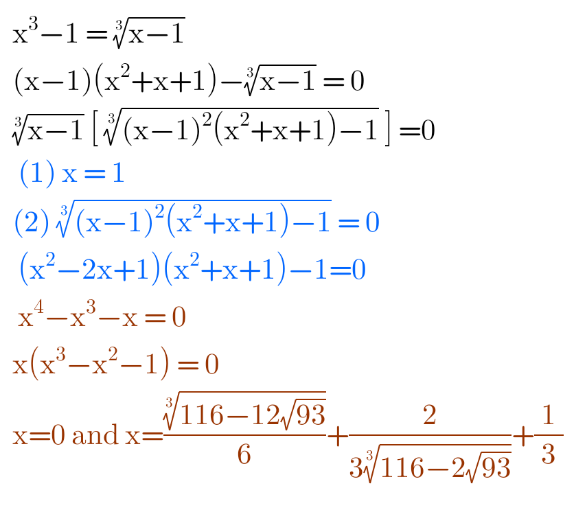
Answered by Frix last updated on 27/Nov/23

1−x^3 =(1−x)^(1/3) (1−x^3 )^3 =1−x x^9 −3x^6 +3x^3 −x=0 x(x−1)(x^3 +x−1)(x^4 +x^3 −2x−1)=0 x=0 x=1 x=(((1/2)+((√(93))/(18))))^(1/3) −((−(1/2)+((√(93))/(18))))^(1/3) ≈.682327804 x=((−1+(√5)−(√(−2+6(√5))))/4)≈−.535687387 x=((−1+(√5)+(√(−2+6(√5))))/4)≈1.15372138

$$\mathrm{1}−{x}^{\mathrm{3}} =\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{3}} \right)^{\mathrm{3}} =\mathrm{1}−{x} \\ $$$${x}^{\mathrm{9}} −\mathrm{3}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{3}} −{x}=\mathrm{0} \\ $$$${x}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{3}} +{x}−\mathrm{1}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} −\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0} \\ $$$${x}=\mathrm{1} \\ $$$${x}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{93}}}{\mathrm{18}}}−\sqrt[{\mathrm{3}}]{−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{93}}}{\mathrm{18}}}\approx.\mathrm{682327804} \\ $$$${x}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}−\sqrt{−\mathrm{2}+\mathrm{6}\sqrt{\mathrm{5}}}}{\mathrm{4}}\approx−.\mathrm{535687387} \\ $$$${x}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}+\sqrt{−\mathrm{2}+\mathrm{6}\sqrt{\mathrm{5}}}}{\mathrm{4}}\approx\mathrm{1}.\mathrm{15372138} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com