
Question Number 200795 by mathlove last updated on 23/Nov/23
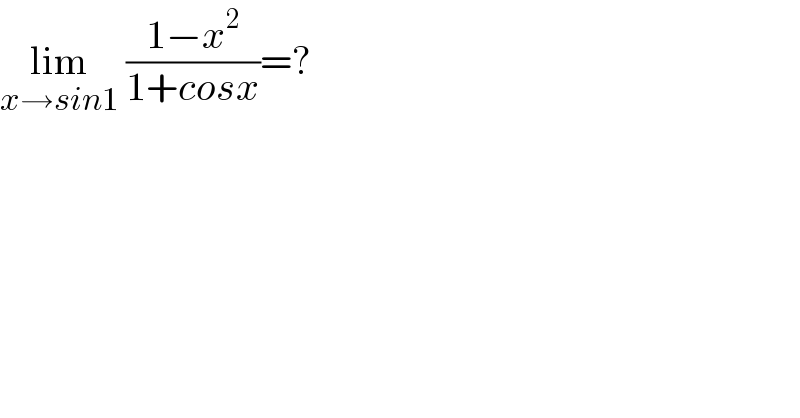
$$\underset{{x}\rightarrow{sin}\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{cosx}}=? \\ $$
Answered by witcher3 last updated on 23/Nov/23
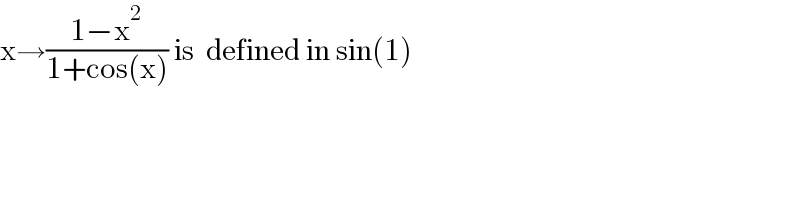
$$\mathrm{x}\rightarrow\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{cos}\left(\mathrm{x}\right)}\:\mathrm{is}\:\:\mathrm{defined}\:\mathrm{in}\:\mathrm{sin}\left(\mathrm{1}\right) \\ $$$$ \\ $$
Commented by mathlove last updated on 23/Nov/23

$${is}\:{sin}\mathrm{1}\approx\mathrm{0}\:\:? \\ $$
Commented by witcher3 last updated on 23/Nov/23

$$\:\frac{\pi}{\mathrm{4}}<\mathrm{1}<\frac{\pi}{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}<\mathrm{sin}\left(\mathrm{1}\right)<\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Commented by Frix last updated on 23/Nov/23
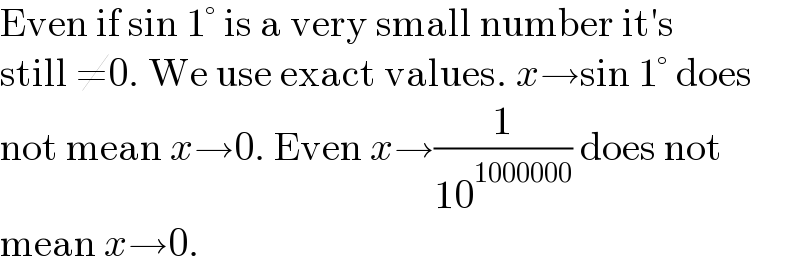
$$\mathrm{Even}\:\mathrm{if}\:\mathrm{sin}\:\mathrm{1}°\:\mathrm{is}\:\mathrm{a}\:\mathrm{very}\:\mathrm{small}\:\mathrm{number}\:\mathrm{it}'\mathrm{s} \\ $$$$\mathrm{still}\:\neq\mathrm{0}.\:\mathrm{We}\:\mathrm{use}\:\mathrm{exact}\:\mathrm{values}.\:{x}\rightarrow\mathrm{sin}\:\mathrm{1}°\:\mathrm{does} \\ $$$$\mathrm{not}\:\mathrm{mean}\:{x}\rightarrow\mathrm{0}.\:\mathrm{Even}\:{x}\rightarrow\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{1000000}} }\:\mathrm{does}\:\mathrm{not} \\ $$$$\mathrm{mean}\:{x}\rightarrow\mathrm{0}. \\ $$
Commented by Frix last updated on 23/Nov/23
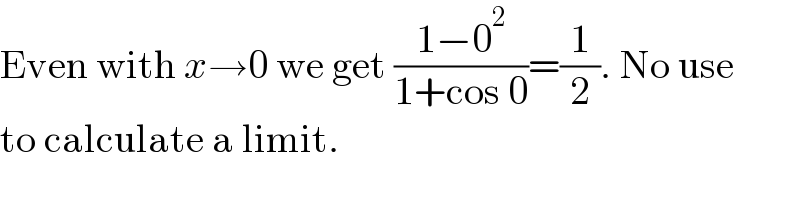
$$\mathrm{Even}\:\mathrm{with}\:{x}\rightarrow\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\frac{\mathrm{1}−\mathrm{0}^{\mathrm{2}} }{\mathrm{1}+\mathrm{cos}\:\mathrm{0}}=\frac{\mathrm{1}}{\mathrm{2}}.\:\mathrm{No}\:\mathrm{use} \\ $$$$\mathrm{to}\:\mathrm{calculate}\:\mathrm{a}\:\mathrm{limit}. \\ $$
