
Question Number 200302 by Calculusboy last updated on 16/Nov/23
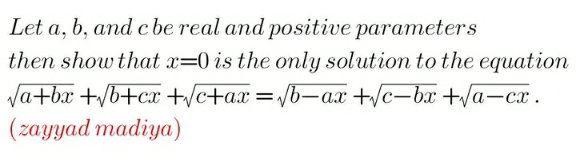
Answered by Rasheed.Sindhi last updated on 18/Nov/23
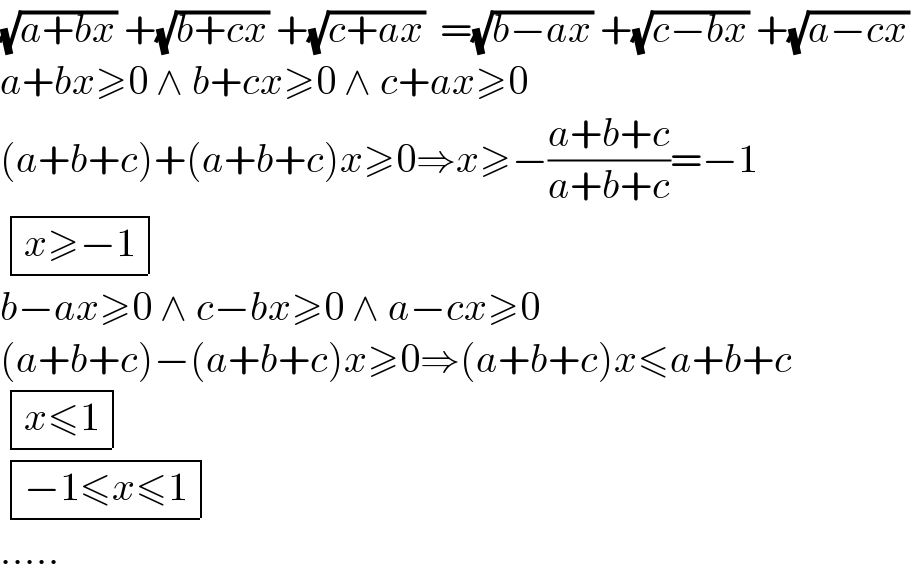
$$\sqrt{{a}+{bx}}\:+\sqrt{{b}+{cx}}\:+\sqrt{{c}+{ax}}\:\:=\sqrt{{b}−{ax}}\:+\sqrt{{c}−{bx}}\:+\sqrt{{a}−{cx}}\: \\ $$$${a}+{bx}\geqslant\mathrm{0}\:\wedge\:{b}+{cx}\geqslant\mathrm{0}\:\wedge\:{c}+{ax}\geqslant\mathrm{0} \\ $$$$\left({a}+{b}+{c}\right)+\left({a}+{b}+{c}\right){x}\geqslant\mathrm{0}\Rightarrow{x}\geqslant−\frac{{a}+{b}+{c}}{{a}+{b}+{c}}=−\mathrm{1} \\ $$$$\begin{array}{|c|}{{x}\geqslant−\mathrm{1}}\\\hline\end{array} \\ $$$${b}−{ax}\geqslant\mathrm{0}\:\wedge\:{c}−{bx}\geqslant\mathrm{0}\:\wedge\:{a}−{cx}\geqslant\mathrm{0} \\ $$$$\left({a}+{b}+{c}\right)−\left({a}+{b}+{c}\right){x}\geqslant\mathrm{0}\Rightarrow\left({a}+{b}+{c}\right){x}\leqslant{a}+{b}+{c} \\ $$$$\begin{array}{|c|}{{x}\leqslant\mathrm{1}}\\\hline\end{array} \\ $$$$\begin{array}{|c|}{−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}}\\\hline\end{array} \\ $$$$..... \\ $$
Commented by Calculusboy last updated on 20/Nov/23

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$
