
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 179948 by mr W last updated on 04/Nov/22
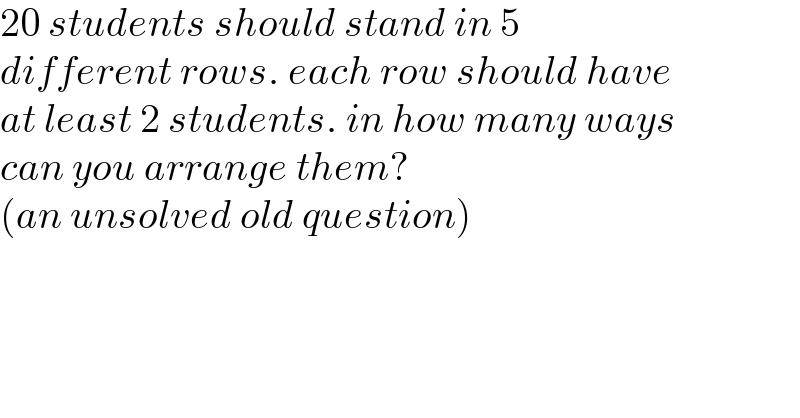
$$\mathrm{20}\:{students}\:{should}\:{stand}\:{in}\:\mathrm{5} \\ $$$${different}\:{rows}.\:{each}\:{row}\:{should}\:{have} \\ $$$${at}\:{least}\:\mathrm{2}\:{students}.\:{in}\:{how}\:{many}\:{ways} \\ $$$${can}\:{you}\:{arrange}\:{them}? \\ $$$$\left({an}\:{unsolved}\:{old}\:{question}\right) \\ $$
Commented by mr W last updated on 04/Nov/22

$${for}\:{test}\:{purpose}\:{we}\:{can}\:{take}\:\mathrm{10}\: \\ $$$${students}\:{in}\:\mathrm{3}\:{rows}. \\ $$
Commented by JDamian last updated on 04/Nov/22
are the students distinguishable?
Commented by mr W last updated on 04/Nov/22

$${yes},\:{we}\:{don}'{t}\:{have}\:{identical}\:{students}. \\ $$
Answered by Frix last updated on 04/Nov/22

$$\mathrm{5}\:\mathrm{rows} \\ $$$$\mathrm{2}\:\mathrm{2}\:\mathrm{2}\:\mathrm{2}\:\mathrm{12}\:×\frac{\mathrm{5}!}{\mathrm{4}!}\:\:\:\:\:\mathrm{2}\:\mathrm{2}\:\mathrm{2}\:\mathrm{3}\:\mathrm{11}\:×\frac{\mathrm{5}!}{\mathrm{3}!}\:\:\:\:\:\mathrm{2}\:\mathrm{2}\:\mathrm{2}\:\mathrm{4}\:\mathrm{10}\:×\frac{\mathrm{5}!}{\mathrm{3}!} \\ $$$$\mathrm{2}\:\mathrm{2}\:\mathrm{2}\:\mathrm{5}\:\mathrm{9}\:×\frac{\mathrm{5}!}{\mathrm{3}!}\:\:\:\:\:\mathrm{2}\:\mathrm{2}\:\mathrm{2}\:\mathrm{6}\:\mathrm{8}\:×\frac{\mathrm{5}!}{\mathrm{3}!}\:\:\:\:\:\mathrm{2}\:\mathrm{2}\:\mathrm{2}\:\mathrm{7}\:\mathrm{7}\:×\frac{\mathrm{5}!}{\mathrm{3}!\mathrm{2}!} \\ $$$$\mathrm{2}\:\mathrm{2}\:\mathrm{3}\:\mathrm{3}\:\mathrm{10}\:×\frac{\mathrm{5}!}{\mathrm{2}!^{\mathrm{2}} }\:\:\:\:\:\mathrm{2}\:\mathrm{2}\:\mathrm{3}\:\mathrm{4}\:\mathrm{9}\:×\frac{\mathrm{5}!}{\mathrm{2}!}\:\:\:\:\:\mathrm{2}\:\mathrm{2}\:\mathrm{3}\:\mathrm{5}\:\mathrm{8}\:×\frac{\mathrm{5}!}{\mathrm{2}!} \\ $$$$\mathrm{2}\:\mathrm{2}\:\mathrm{3}\:\mathrm{6}\:\mathrm{7}\:×\frac{\mathrm{5}!}{\mathrm{2}!}\:\:\:\:\:\mathrm{2}\:\mathrm{2}\:\mathrm{4}\:\mathrm{4}\:\mathrm{8}\:×\frac{\mathrm{5}!}{\mathrm{2}!^{\mathrm{2}} }\:\:\:\:\:\mathrm{2}\:\mathrm{2}\:\mathrm{4}\:\mathrm{5}\:\mathrm{7}\:×\frac{\mathrm{5}!}{\mathrm{2}!} \\ $$$$\mathrm{2}\:\mathrm{2}\:\mathrm{4}\:\mathrm{6}\:\mathrm{6}\:×\frac{\mathrm{5}!}{\mathrm{2}!^{\mathrm{2}} }\:\:\:\:\:\mathrm{2}\:\mathrm{2}\:\mathrm{5}\:\mathrm{5}\:\mathrm{6}\:×\frac{\mathrm{5}!}{\mathrm{2}!^{\mathrm{2}} }\:\:\:\:\:\mathrm{2}\:\mathrm{3}\:\mathrm{3}\:\mathrm{3}\:\mathrm{9}\:×\frac{\mathrm{5}!}{\mathrm{3}!} \\ $$$$\mathrm{2}\:\mathrm{3}\:\mathrm{3}\:\mathrm{4}\:\mathrm{8}\:×\frac{\mathrm{5}!}{\mathrm{2}!}\:\:\:\:\:\mathrm{2}\:\mathrm{3}\:\mathrm{3}\:\mathrm{5}\:\mathrm{7}\:×\frac{\mathrm{5}!}{\mathrm{2}!}\:\:\:\:\:\mathrm{2}\:\mathrm{3}\:\mathrm{3}\:\mathrm{6}\:\mathrm{6}\:×\frac{\mathrm{5}!}{\mathrm{2}!^{\mathrm{2}} } \\ $$$$\mathrm{2}\:\mathrm{3}\:\mathrm{4}\:\mathrm{4}\:\mathrm{7}\:×\frac{\mathrm{5}!}{\mathrm{2}!}\:\:\:\:\:\mathrm{2}\:\mathrm{3}\:\mathrm{4}\:\mathrm{5}\:\mathrm{6}\:×\mathrm{5}!\:\:\:\:\:\mathrm{2}\:\mathrm{3}\:\mathrm{5}\:\mathrm{5}\:\mathrm{5}\:×\frac{\mathrm{5}!}{\mathrm{3}!} \\ $$$$\mathrm{2}\:\mathrm{4}\:\mathrm{4}\:\mathrm{4}\:\mathrm{6}\:×\frac{\mathrm{5}!}{\mathrm{3}!}\:\:\:\:\:\mathrm{2}\:\mathrm{4}\:\mathrm{4}\:\mathrm{5}\:\mathrm{5}\:×\frac{\mathrm{5}!}{\mathrm{2}!^{\mathrm{2}} }\:\:\:\:\:\mathrm{3}\:\mathrm{3}\:\mathrm{3}\:\mathrm{3}\:\mathrm{8}\:×\frac{\mathrm{5}!}{\mathrm{4}!} \\ $$$$\mathrm{3}\:\mathrm{3}\:\mathrm{3}\:\mathrm{4}\:\mathrm{7}\:×\frac{\mathrm{5}!}{\mathrm{3}!}\:\:\:\:\:\mathrm{3}\:\mathrm{3}\:\mathrm{3}\:\mathrm{5}\:\mathrm{6}\:×\frac{\mathrm{5}!}{\mathrm{3}!}\:\:\:\:\:\mathrm{3}\:\mathrm{3}\:\mathrm{4}\:\mathrm{4}\:\mathrm{6}\:×\frac{\mathrm{5}!}{\mathrm{2}!^{\mathrm{2}} } \\ $$$$\mathrm{3}\:\mathrm{3}\:\mathrm{4}\:\mathrm{5}\:\mathrm{5}\:×\frac{\mathrm{5}!}{\mathrm{2}!^{\mathrm{2}} }\:\:\:\:\:\mathrm{3}\:\mathrm{4}\:\mathrm{4}\:\mathrm{4}\:\mathrm{5}\:×\frac{\mathrm{5}!}{\mathrm{3}!}\:\:\:\:\:\mathrm{4}\:\mathrm{4}\:\mathrm{4}\:\mathrm{4}\:\mathrm{4}\:×\frac{\mathrm{5}!}{\mathrm{5}!} \\ $$$$\mathrm{1001}\:\mathrm{possibilities} \\ $$$$\mathrm{20}\:\mathrm{students}\:=\:\mathrm{20}!\:\mathrm{possibilities} \\ $$$$\mathrm{total}: \\ $$$$\mathrm{1001}×\mathrm{20}!=\mathrm{2}\:\mathrm{435}\:\mathrm{334}\:\mathrm{910}\:\mathrm{184}\:\mathrm{816}\:\mathrm{640}\:\mathrm{000} \\ $$
Commented by mr W last updated on 05/Nov/22
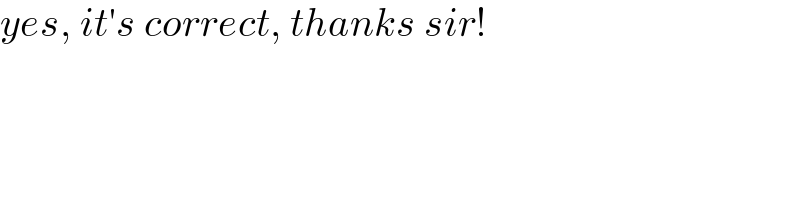
$${yes},\:{it}'{s}\:{correct},\:{thanks}\:{sir}! \\ $$
Commented by mr W last updated on 05/Nov/22

$${the}\:{number}\:{is}\:{so}\:{terribly}\:{huge}! \\ $$$${the}\:{question}\:{is}\:{the}\:{same}\:{as}\:{in}\:{how} \\ $$$${many}\:{ways}\:{we}\:{can}\:{arrange}\:\mathrm{20}\:{books} \\ $$$${in}\:{a}\:{book}\:{rack}\:{with}\:\mathrm{5}\:{shelves}. \\ $$$${say}\:{we}\:{can}\:{work}\:{very}\:{quickly}\:{and} \\ $$$${need}\:{only}\:{one}\:{second}\:{for}\:{each}\: \\ $$$${arrangement},\:{and}\:{we}\:{began}\:{to}\:{work} \\ $$$${as}\:{the}\:{universe}\:{began}\:{to}\:{exist},\:{i}.{e}. \\ $$$${as}\:{the}\:{big}\:{bang}\:{occurred}.\:{what}\:{do}\:{you} \\ $$$${think}?\:{have}\:{we}\:{done}\:{all}\:{the}\:{possible} \\ $$$${arrangements}?\: \\ $$$${no}!\:{no}\:{by}\:{far}!\:{in}\:{fact}\:{we}\:{haven}'{t}\:{even} \\ $$$${done}\:\mathrm{0}.\mathrm{02\%}\:{of}\:{the}\:{work}\:{yet}! \\ $$$${not}\:{to}\:{think},\:{what}\:{when}\:{we}\:{have}\: \\ $$$$\mathrm{100}\:{books}! \\ $$
Commented by mr W last updated on 05/Nov/22

Answered by mr W last updated on 05/Nov/22
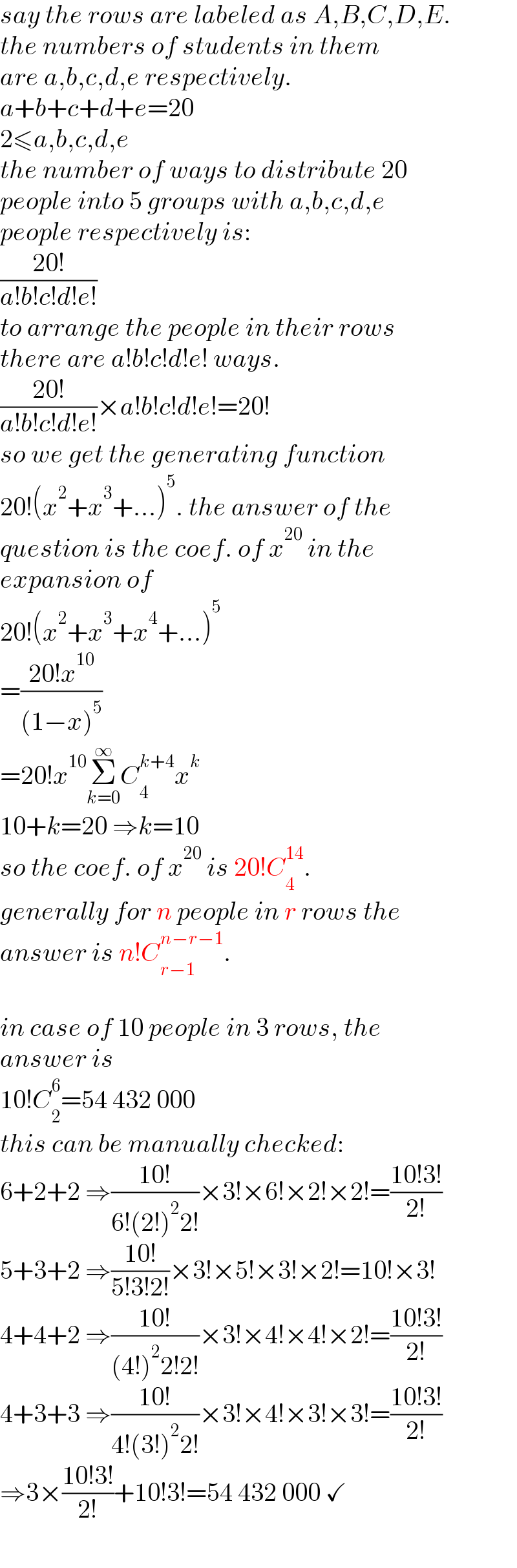
$${say}\:{the}\:{rows}\:{are}\:{labeled}\:{as}\:{A},{B},{C},{D},{E}. \\ $$$${the}\:{numbers}\:{of}\:{students}\:{in}\:{them} \\ $$$${are}\:{a},{b},{c},{d},{e}\:{respectively}. \\ $$$${a}+{b}+{c}+{d}+{e}=\mathrm{20} \\ $$$$\mathrm{2}\leqslant{a},{b},{c},{d},{e} \\ $$$${the}\:{number}\:{of}\:{ways}\:{to}\:{distribute}\:\mathrm{20}\: \\ $$$${people}\:{into}\:\mathrm{5}\:{groups}\:{with}\:{a},{b},{c},{d},{e}\: \\ $$$${people}\:{respectively}\:{is}: \\ $$$$\frac{\mathrm{20}!}{{a}!{b}!{c}!{d}!{e}!} \\ $$$${to}\:{arrange}\:{the}\:{people}\:{in}\:{their}\:{rows} \\ $$$${there}\:{are}\:{a}!{b}!{c}!{d}!{e}!\:{ways}. \\ $$$$\frac{\mathrm{20}!}{{a}!{b}!{c}!{d}!{e}!}×{a}!{b}!{c}!{d}!{e}!=\mathrm{20}! \\ $$$${so}\:{we}\:{get}\:{the}\:{generating}\:{function} \\ $$$$\mathrm{20}!\left({x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...\right)^{\mathrm{5}} .\:{the}\:{answer}\:{of}\:{the} \\ $$$${question}\:{is}\:{the}\:{coef}.\:{of}\:{x}^{\mathrm{20}} \:{in}\:{the} \\ $$$${expansion}\:{of}\: \\ $$$$\mathrm{20}!\left({x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +...\right)^{\mathrm{5}} \\ $$$$=\frac{\mathrm{20}!{x}^{\mathrm{10}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{5}} } \\ $$$$=\mathrm{20}!{x}^{\mathrm{10}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{4}} ^{{k}+\mathrm{4}} {x}^{{k}} \\ $$$$\mathrm{10}+{k}=\mathrm{20}\:\Rightarrow{k}=\mathrm{10} \\ $$$${so}\:{the}\:{coef}.\:{of}\:{x}^{\mathrm{20}} \:{is}\:\mathrm{20}!{C}_{\mathrm{4}} ^{\mathrm{14}} . \\ $$$${generally}\:{for}\:{n}\:{people}\:{in}\:{r}\:{rows}\:{the} \\ $$$${answer}\:{is}\:{n}!{C}_{{r}−\mathrm{1}} ^{{n}−{r}−\mathrm{1}} . \\ $$$$ \\ $$$${in}\:{case}\:{of}\:\mathrm{10}\:{people}\:{in}\:\mathrm{3}\:{rows},\:{the} \\ $$$${answer}\:{is} \\ $$$$\mathrm{10}!{C}_{\mathrm{2}} ^{\mathrm{6}} =\mathrm{54}\:\mathrm{432}\:\mathrm{000} \\ $$$${this}\:{can}\:{be}\:{manually}\:{checked}: \\ $$$$\mathrm{6}+\mathrm{2}+\mathrm{2}\:\Rightarrow\frac{\mathrm{10}!}{\mathrm{6}!\left(\mathrm{2}!\right)^{\mathrm{2}} \mathrm{2}!}×\mathrm{3}!×\mathrm{6}!×\mathrm{2}!×\mathrm{2}!=\frac{\mathrm{10}!\mathrm{3}!}{\mathrm{2}!} \\ $$$$\mathrm{5}+\mathrm{3}+\mathrm{2}\:\Rightarrow\frac{\mathrm{10}!}{\mathrm{5}!\mathrm{3}!\mathrm{2}!}×\mathrm{3}!×\mathrm{5}!×\mathrm{3}!×\mathrm{2}!=\mathrm{10}!×\mathrm{3}! \\ $$$$\mathrm{4}+\mathrm{4}+\mathrm{2}\:\Rightarrow\frac{\mathrm{10}!}{\left(\mathrm{4}!\right)^{\mathrm{2}} \mathrm{2}!\mathrm{2}!}×\mathrm{3}!×\mathrm{4}!×\mathrm{4}!×\mathrm{2}!=\frac{\mathrm{10}!\mathrm{3}!}{\mathrm{2}!} \\ $$$$\mathrm{4}+\mathrm{3}+\mathrm{3}\:\Rightarrow\frac{\mathrm{10}!}{\mathrm{4}!\left(\mathrm{3}!\right)^{\mathrm{2}} \mathrm{2}!}×\mathrm{3}!×\mathrm{4}!×\mathrm{3}!×\mathrm{3}!=\frac{\mathrm{10}!\mathrm{3}!}{\mathrm{2}!} \\ $$$$\Rightarrow\mathrm{3}×\frac{\mathrm{10}!\mathrm{3}!}{\mathrm{2}!}+\mathrm{10}!\mathrm{3}!=\mathrm{54}\:\mathrm{432}\:\mathrm{000}\:\checkmark \\ $$
Commented by mr W last updated on 05/Nov/22

$${alternative}\:{way}\:{instead}\:{of}\:{using} \\ $$$${generating}\:{function}: \\ $$$${a}+{b}+{c}+{d}+{e}=\mathrm{20} \\ $$$$\mathrm{2}\leqslant{a},{b},{c},{d},{e} \\ $$$${let}\:{a}={a}'+\mathrm{1},\:{b}={b}'+\mathrm{1},\:... \\ $$$${a}'+{b}'+{c}'+{d}'+{e}'=\mathrm{15} \\ $$$$\mathrm{1}\leqslant{a}',{b}',{c}',{d}',{e}' \\ $$$$\bigstar\mid\bigstar\mid\bigstar\mid\bigstar\mid\bigstar\mid\bigstar\mid\bigstar...\bigstar\mid\bigstar\mid\bigstar \\ $$$$\left(\mathrm{15}\:{stars}\:{and}\:\mathrm{14}\:{bars}\right) \\ $$$${the}\:{number}\:{of}\:{ways}\:{to}\:{select}\:\mathrm{4}\:{of}\:{the} \\ $$$$\mathrm{14}\:{bars}\:{is}\:{C}_{\mathrm{4}} ^{\mathrm{14}} =\mathrm{1001}.\:{so}\:{the}\:{answer}\:{is} \\ $$$$\mathrm{20}!{C}_{\mathrm{4}} ^{\mathrm{14}} =\mathrm{1001}×\mathrm{20}! \\ $$
Commented by Frix last updated on 05/Nov/22

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{explaining} \\ $$
