Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 215227 by Ghisom last updated on 01/Jan/25

(20+25)^2 =2025 only 3 other 4 digit numbers: (00+01)^2 =0001 (30+25)^2 =3025 (98+01)^2 =9801

$$\left(\mathrm{20}+\mathrm{25}\right)^{\mathrm{2}} =\mathrm{2025} \\ $$$$\mathrm{only}\:\mathrm{3}\:\mathrm{other}\:\mathrm{4}\:\mathrm{digit}\:\mathrm{numbers}: \\ $$$$\left(\mathrm{00}+\mathrm{01}\right)^{\mathrm{2}} =\mathrm{0001} \\ $$$$\left(\mathrm{30}+\mathrm{25}\right)^{\mathrm{2}} =\mathrm{3025} \\ $$$$\left(\mathrm{98}+\mathrm{01}\right)^{\mathrm{2}} =\mathrm{9801} \\ $$

Answered by Rasheed.Sindhi last updated on 01/Jan/25

determinant (((How to determine such numbers))) (a+b)^2 =100a+b ; a,b are 2-digit numbers a^2 +2ab+b^2 −100a−b=0 a^2 +(2b−100)a+b^2 −b=0 a=((100−2b±(√((2b−100)^2 −4(b^2 −b))))/(2a)) a=((100−2b±2(√((b−50)^2 −(b^2 −b))))/2) =50−b±(√(b^2 −100b+2500−b^2 +b)) =50−b±(√(2500−99b)) ; 00≤b≤25 2500−99b=p^2 ⇒b=00,01,25 b=00 a=50−b±(√(2500−99b)) a=50−0±50=100^(×) , 00 0000 b=01 a=50−1±49=98 , 00 0001 , 9801 b=25 a=25±25=50,00 =50−25±5 30 or 20 3025 ,2025

$$\begin{array}{|c|}{\mathcal{H}{ow}\:{to}\:{determine}\:{such}\:{numbers}}\\\hline\end{array} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} =\mathrm{100}{a}+{b}\:;\:{a},{b}\:{are}\:\mathrm{2}-{digit}\:{numbers} \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} −\mathrm{100}{a}−{b}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} +\left(\mathrm{2}{b}−\mathrm{100}\right){a}+{b}^{\mathrm{2}} −{b}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{100}−\mathrm{2}{b}\pm\sqrt{\left(\mathrm{2}{b}−\mathrm{100}\right)^{\mathrm{2}} −\mathrm{4}\left({b}^{\mathrm{2}} −{b}\right)}}{\mathrm{2}{a}} \\ $$$${a}=\frac{\mathrm{100}−\mathrm{2}{b}\pm\mathrm{2}\sqrt{\left({b}−\mathrm{50}\right)^{\mathrm{2}} −\left({b}^{\mathrm{2}} −{b}\right)}}{\mathrm{2}} \\ $$$$\:\:\:=\mathrm{50}−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{100}{b}+\mathrm{2500}−{b}^{\mathrm{2}} +{b}} \\ $$$$\:\:\:=\mathrm{50}−{b}\pm\sqrt{\mathrm{2500}−\mathrm{99}{b}}\:;\:\mathrm{00}\leqslant{b}\leqslant\mathrm{25} \\ $$$$\:\:\:\:\:\:\mathrm{2500}−\mathrm{99}{b}={p}^{\mathrm{2}} \Rightarrow{b}=\mathrm{00},\mathrm{01},\mathrm{25} \\ $$$${b}=\mathrm{00} \\ $$$$\:{a}=\mathrm{50}−{b}\pm\sqrt{\mathrm{2500}−\mathrm{99}{b}}\: \\ $$$${a}=\mathrm{50}−\mathrm{0}\pm\mathrm{50}=\overset{×} {\mathrm{100}}\:,\:\mathrm{00} \\ $$$$\mathrm{0000} \\ $$$${b}=\mathrm{01} \\ $$$${a}=\mathrm{50}−\mathrm{1}\pm\mathrm{49}=\mathrm{98}\:,\:\mathrm{00} \\ $$$$\mathrm{0001}\:,\:\mathrm{9801} \\ $$$${b}=\mathrm{25} \\ $$$${a}=\mathrm{25}\pm\mathrm{25}=\mathrm{50},\mathrm{00} \\ $$$$\:\:\:=\mathrm{50}−\mathrm{25}\pm\mathrm{5} \\ $$$$\:\:\:\:\:\mathrm{30}\:{or}\:\mathrm{20} \\ $$$$\mathrm{3025}\:,\mathrm{2025} \\ $$

Commented by MathematicalUser2357 last updated on 08/Jan/25

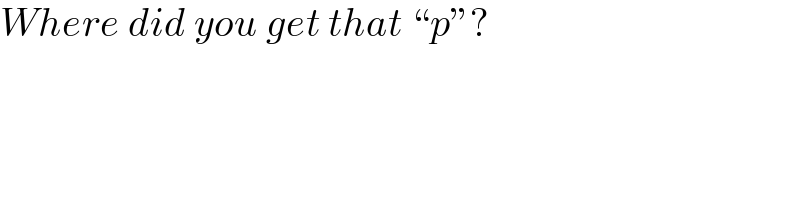
Where did you get that “p”?

$${Where}\:{did}\:{you}\:{get}\:{that}\:``{p}''? \\ $$

Answered by MrGaster last updated on 01/Jan/25

(20+25)^2 =2025 (45)^2 =2025

$$\cancel{\left(\mathrm{20}+\mathrm{25}\right)^{\mathrm{2}} =\mathrm{2025}} \\ $$$$\left(\mathrm{45}\right)^{\mathrm{2}} =\mathrm{2025} \\ $$

Commented by Frix last updated on 01/Jan/25

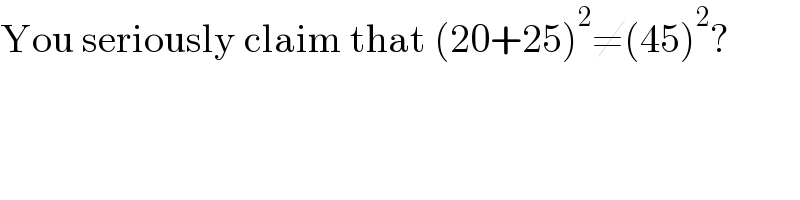
You seriously claim that (20+25)^2 ≠(45)^2 ?

$$\mathrm{You}\:\mathrm{seriously}\:\mathrm{claim}\:\mathrm{that}\:\left(\mathrm{20}+\mathrm{25}\right)^{\mathrm{2}} \neq\left(\mathrm{45}\right)^{\mathrm{2}} ? \\ $$

Commented by MrGaster last updated on 01/Jan/25

Sorry, my fault.

Terms of Service

Privacy Policy

Contact: info@tinkutara.com