
Question Number 198400 by cortano12 last updated on 19/Oct/23

$$\:\:\mathrm{20}^{\mathrm{11}} −\mathrm{1}\:=\:...\left(\mathrm{mod}\:\mathrm{1000}\right) \\ $$
Answered by MM42 last updated on 19/Oct/23

$$\mathrm{20}^{\mathrm{11}} −\mathrm{1}\overset{\mathrm{1000}} {\equiv}−\mathrm{1}\overset{\mathrm{1000}} {\equiv}\mathrm{999} \\ $$
Answered by mr W last updated on 19/Oct/23

$$\mathrm{20}^{\mathrm{11}} =\mathrm{2}^{\mathrm{11}} ×\mathrm{10}^{\mathrm{11}} =\mathrm{204800000000000} \\ $$$$\mathrm{20}^{\mathrm{11}} −\mathrm{1}=\mathrm{204799999999999} \\ $$$$... \\ $$
Answered by BaliramKumar last updated on 19/Oct/23
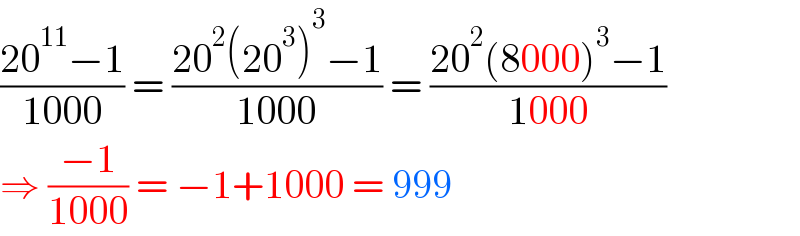
$$\frac{\mathrm{20}^{\mathrm{11}} −\mathrm{1}}{\mathrm{1000}}\:=\:\frac{\mathrm{20}^{\mathrm{2}} \left(\mathrm{20}^{\mathrm{3}} \right)^{\mathrm{3}} −\mathrm{1}}{\mathrm{1000}}\:=\:\frac{\mathrm{20}^{\mathrm{2}} \left(\mathrm{8000}\right)^{\mathrm{3}} −\mathrm{1}}{\mathrm{1000}}\: \\ $$$$\Rightarrow\:\frac{−\mathrm{1}}{\mathrm{1000}}\:=\:−\mathrm{1}+\mathrm{1000}\:=\:\mathrm{999}\: \\ $$
