
Question Number 184376 by Ml last updated on 05/Jan/23

$$\mathrm{2}^{\mathrm{x}} =\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{x}=\mathrm{2} \\ $$$$\mathrm{x}=\mathrm{4} \\ $$$$\mathrm{x}=−\mathrm{0}.\mathrm{76666} \\ $$$$??????????????????? \\ $$$$\mathrm{solution}\:\mathrm{please} \\ $$
Answered by Frix last updated on 05/Jan/23
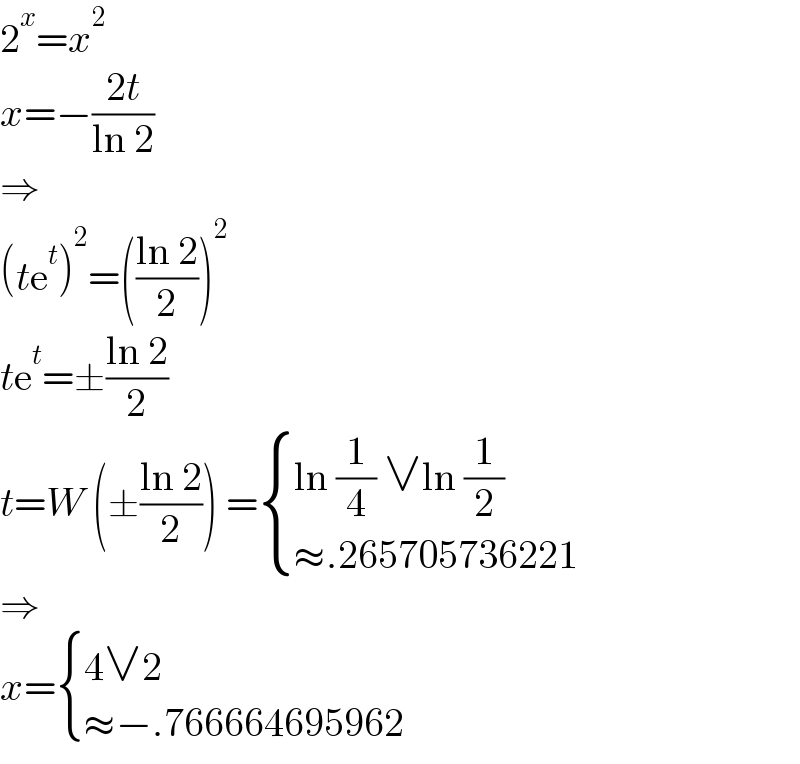
$$\mathrm{2}^{{x}} ={x}^{\mathrm{2}} \\ $$$${x}=−\frac{\mathrm{2}{t}}{\mathrm{ln}\:\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\left({t}\mathrm{e}^{{t}} \right)^{\mathrm{2}} =\left(\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${t}\mathrm{e}^{{t}} =\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}} \\ $$$${t}={W}\:\left(\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)\:=\begin{cases}{\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{4}}\:\vee\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{2}}}\\{\approx.\mathrm{265705736221}}\end{cases} \\ $$$$\Rightarrow \\ $$$${x}=\begin{cases}{\mathrm{4}\vee\mathrm{2}}\\{\approx−.\mathrm{766664695962}}\end{cases} \\ $$
