Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 206536 by cortano21 last updated on 18/Apr/24

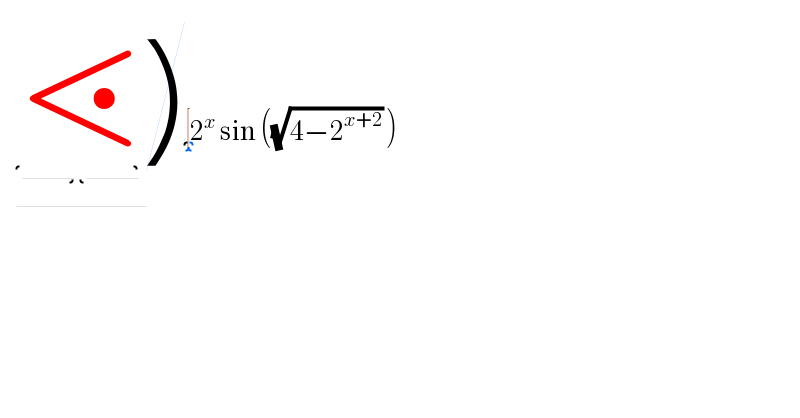
⋖ ♠[2^x sin ((√(4−2^(x+2) )) )

$$\:\:\:\:\underline{\underbrace{\lessdot}\cancel{} }\underbrace{\nsupseteqq\spadesuit\left[}\mathrm{2}^{{x}} \:\mathrm{sin}\:\left(\sqrt{\mathrm{4}−\mathrm{2}^{{x}+\mathrm{2}} }\:\right)\right. \\ $$

Commented by Frix last updated on 18/Apr/24

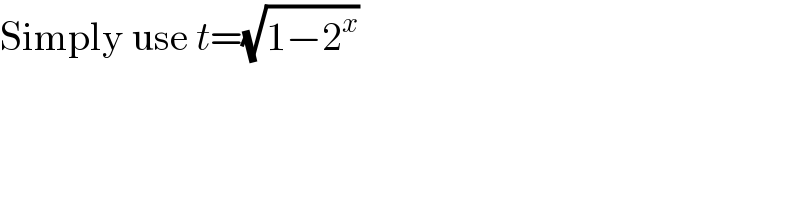
Simply use t=(√(1−2^x ))

$$\mathrm{Simply}\:\mathrm{use}\:{t}=\sqrt{\mathrm{1}−\mathrm{2}^{{x}} } \\ $$

Answered by lepuissantcedricjunior last updated on 20/Apr/24

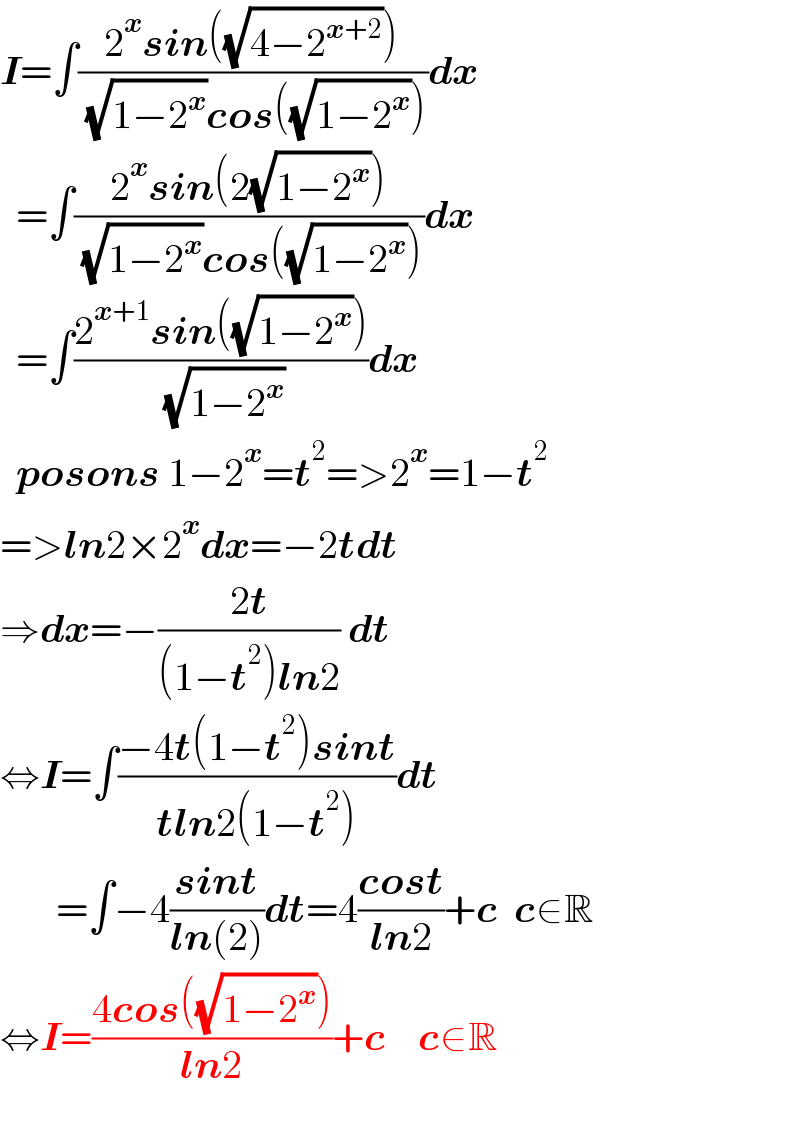
I=∫((2^x sin((√(4−2^(x+2) ))))/( (√(1−2^x ))cos((√(1−2^x )))))dx =∫((2^x sin(2(√(1−2^x ))))/( (√(1−2^x ))cos((√(1−2^x )))))dx =∫((2^(x+1) sin((√(1−2^x ))))/( (√(1−2^x ))))dx posons 1−2^x =t^2 =>2^x =1−t^2 =>ln2×2^x dx=−2tdt ⇒dx=−((2t)/((1−t^2 )ln2)) dt ⇔I=∫((−4t(1−t^2 )sint)/(tln2(1−t^2 )))dt =∫−4((sint)/(ln(2)))dt=4((cost)/(ln2))+c c∈R ⇔I=((4cos((√(1−2^x ))))/(ln2))+c c∈R

$$\boldsymbol{{I}}=\int\frac{\mathrm{2}^{\boldsymbol{{x}}} \boldsymbol{{sin}}\left(\sqrt{\mathrm{4}−\mathrm{2}^{\boldsymbol{{x}}+\mathrm{2}} }\right)}{\:\sqrt{\mathrm{1}−\mathrm{2}^{\boldsymbol{{x}}} }\boldsymbol{{cos}}\left(\sqrt{\mathrm{1}−\mathrm{2}^{\boldsymbol{{x}}} }\right)}\boldsymbol{{dx}} \\ $$$$\:\:=\int\frac{\mathrm{2}^{\boldsymbol{{x}}} \boldsymbol{{sin}}\left(\mathrm{2}\sqrt{\mathrm{1}−\mathrm{2}^{\boldsymbol{{x}}} }\right)}{\:\sqrt{\mathrm{1}−\mathrm{2}^{\boldsymbol{{x}}} }\boldsymbol{{cos}}\left(\sqrt{\mathrm{1}−\mathrm{2}^{\boldsymbol{{x}}} }\right)}\boldsymbol{{dx}} \\ $$$$\:\:=\int\frac{\mathrm{2}^{\boldsymbol{{x}}+\mathrm{1}} \boldsymbol{{sin}}\left(\sqrt{\mathrm{1}−\mathrm{2}^{\boldsymbol{{x}}} }\right)}{\:\sqrt{\mathrm{1}−\mathrm{2}^{\boldsymbol{{x}}} }}\boldsymbol{{dx}} \\ $$$$\:\:\boldsymbol{{posons}}\:\mathrm{1}−\mathrm{2}^{\boldsymbol{{x}}} =\boldsymbol{{t}}^{\mathrm{2}} =>\mathrm{2}^{\boldsymbol{{x}}} =\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} \\ $$$$=>\boldsymbol{{ln}}\mathrm{2}×\mathrm{2}^{\boldsymbol{{x}}} \boldsymbol{{dx}}=−\mathrm{2}\boldsymbol{{tdt}} \\ $$$$\Rightarrow\boldsymbol{{dx}}=−\frac{\mathrm{2}\boldsymbol{{t}}}{\left(\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} \right)\boldsymbol{{ln}}\mathrm{2}}\:\boldsymbol{{dt}} \\ $$$$\Leftrightarrow\boldsymbol{{I}}=\int\frac{−\mathrm{4}\boldsymbol{{t}}\left(\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} \right)\boldsymbol{{sint}}}{\boldsymbol{{tln}}\mathrm{2}\left(\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} \right)}\boldsymbol{{dt}} \\ $$$$\:\:\:\:\:\:\:=\int−\mathrm{4}\frac{\boldsymbol{{sint}}}{\boldsymbol{{ln}}\left(\mathrm{2}\right)}\boldsymbol{{dt}}=\mathrm{4}\frac{\boldsymbol{{cost}}}{\boldsymbol{{ln}}\mathrm{2}}+\boldsymbol{{c}}\:\:\boldsymbol{{c}}\in\mathbb{R} \\ $$$$\Leftrightarrow\boldsymbol{{I}}=\frac{\mathrm{4}\boldsymbol{{cos}}\left(\sqrt{\mathrm{1}−\mathrm{2}^{\boldsymbol{{x}}} }\right)}{\boldsymbol{{ln}}\mathrm{2}}+\boldsymbol{{c}}\:\:\:\:\boldsymbol{{c}}\in\mathbb{R} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com