
Question Number 143706 by Huy last updated on 17/Jun/21
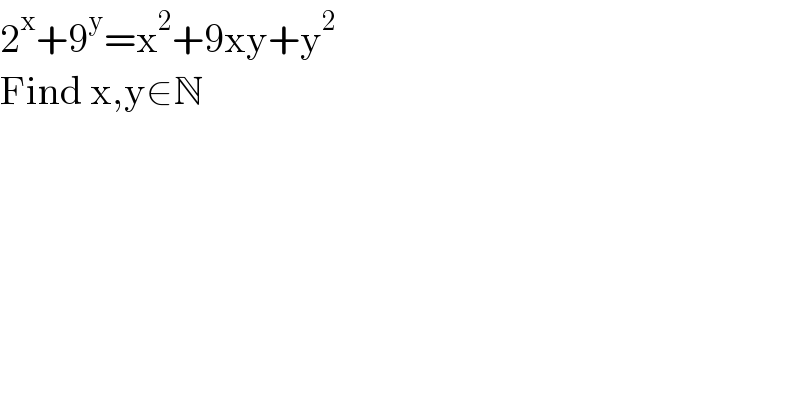
$$\mathrm{2}^{\mathrm{x}} +\mathrm{9}^{\mathrm{y}} =\mathrm{x}^{\mathrm{2}} +\mathrm{9xy}+\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{Find}\:\mathrm{x},\mathrm{y}\in\mathbb{N} \\ $$
Answered by TheHoneyCat last updated on 17/Jun/21
![for x=10 we get: 1024+9^y =^? 100+90y+y^2 checking in y=10 and studing the derivative one gets: ∀y≥10, 1024+9^y >100+90y+y^2 looking at how the values evolve for x (the derivative for x) we get also that ∀x,y≥10 2^x +9^y >x^2 +9xy+y^2 Checking, with a computer, for all the values (x,y)∈[∣0,10∣]^2 I found that there are only two possibilites: (x,y)∈{(1,1);(3,0)} by the way, it is surely possible to get a better maximum value than ′′10′′ so that the verification can be done by hand I was just too lazy to do it efficiently](Q143716.png)
$$ \\ $$$$\mathrm{for}\:{x}=\mathrm{10}\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{1024}+\mathrm{9}^{{y}} \overset{?} {=}\mathrm{100}+\mathrm{90}{y}+{y}^{\mathrm{2}} \\ $$$$\mathrm{checking}\:\mathrm{in}\:{y}=\mathrm{10}\:\mathrm{and}\:\mathrm{studing}\:\mathrm{the}\:\mathrm{derivative} \\ $$$$\mathrm{one}\:\mathrm{gets}: \\ $$$$ \\ $$$$\forall{y}\geqslant\mathrm{10},\:\mathrm{1024}+\mathrm{9}^{{y}} >\mathrm{100}+\mathrm{90}{y}+{y}^{\mathrm{2}} \\ $$$$\mathrm{looking}\:\mathrm{at}\:\mathrm{how}\:\mathrm{the}\:\mathrm{values}\:\mathrm{evolve}\:\mathrm{for}\:{x}\:\left({the}\:{derivative}\:{for}\:{x}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{also}\:\mathrm{that}\:\forall{x},{y}\geqslant\mathrm{10}\:\mathrm{2}^{{x}} +\mathrm{9}^{{y}} >{x}^{\mathrm{2}} +\mathrm{9}{xy}+{y}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Checking},\:\mathrm{with}\:\mathrm{a}\:\mathrm{computer},\:\mathrm{for}\:\mathrm{all}\:\mathrm{the}\:\mathrm{values}\:\left({x},{y}\right)\in\left[\mid\mathrm{0},\mathrm{10}\mid\right]^{\mathrm{2}} \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{that}\:\mathrm{there}\:\mathrm{are}\:\mathrm{only}\:\mathrm{two}\:\mathrm{possibilites}: \\ $$$$\left({x},{y}\right)\in\left\{\left(\mathrm{1},\mathrm{1}\right);\left(\mathrm{3},\mathrm{0}\right)\right\} \\ $$$$ \\ $$$$ \\ $$$${by}\:{the}\:{way},\:{it}\:{is}\:{surely}\:{possible}\:{to}\:{get}\:{a}\:{better}\:{maximum}\:{value}\:{than}\:''\mathrm{10}'' \\ $$$${so}\:{that}\:{the}\:{verification}\:{can}\:{be}\:{done}\:{by}\:{hand} \\ $$$${I}\:{was}\:{just}\:{too}\:{lazy}\:{to}\:{do}\:{it}\:{efficiently} \\ $$
