Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 5764 by sanusihammed last updated on 26/May/16

2^x = 4x Solution 2^x = 4x This can be re write as (1+1)^x = 4x Using combination to epand from the identity. (1+x)^n = 1+nx+((n(n−1))/(2!))x^2 +((n(n−1)(n−2))/(3!))x^3 +....+nCrx^(r ) Therefore. (1+1)^x = 4x 1+x+((x(x−1))/(2!))(1^2 )+((x(x−1)(x−2))/(3!))(1^3 )+......+1 = 4x ignore the continuity (what rule is ..... ignore the +...+) is it linear approximation 1+x+((x^2 −x)/(2×1))+(((x^2 −x)(x−2))/(3×2×1))+1 = 4x 1+x+((x^2 −x)/2)+((x^3 −2x^2 −x^2 +2x)/6)+1 = 4x 1+x+((x^2 −x)/2)+((x^3 −3x^2 +2x)/6)+1 = 4x Multiply through by 6 6+6x+3(x^2 −x)+x^3 −3x^2 +2x+6 = 24x 12+6x+3x^2 −3x+x^3 −3x^2 +2x+6 = 24x 12+5x+x^3 = 24x 12+5x+x^3 −24x = 0 x^3 −19x+12 = 0 Factorize x^3 −4x^2 +4x^2 −16x−3x+12 = 0 (x^3 −4x^2 )+(4x^2 −16x)−(3x+12) = 0 x^2 (x−4)+4x(x−4)−3(x−4) = 0 Factor out (x−4) (x−4)(x^2 +4x−3) = 0 x−4 = 0 or x^( 2) +4x−3 = 0 x = 4 or x = 0.6458 or x = −4.6458 The only real solution is x = 4 Therefore x = 4 DONE! Please confirm the solution. is it correct or please corect it or show me alternative. This is my trial. Thanks.

$$\mathrm{2}^{{x}} \:=\:\mathrm{4}{x} \\ $$$${Solution} \\ $$$$\mathrm{2}^{{x}} \:=\:\mathrm{4}{x} \\ $$$${This}\:{can}\:{be}\:{re}\:{write}\:{as} \\ $$$$\left(\mathrm{1}+\mathrm{1}\right)^{{x}} \:=\:\mathrm{4}{x} \\ $$$${Using}\:{combination}\:{to}\:{epand} \\ $$$${from}\:{the}\:{identity}. \\ $$$$\left(\mathrm{1}+{x}\right)^{{n}} \:=\:\mathrm{1}+{nx}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{3}!}{x}^{\mathrm{3}} +....+{nCrx}^{{r}\:} \: \\ $$$${Therefore}. \\ $$$$\left(\mathrm{1}+\mathrm{1}\right)^{{x}} \:=\:\mathrm{4}{x} \\ $$$$\mathrm{1}+{x}+\frac{{x}\left({x}−\mathrm{1}\right)}{\mathrm{2}!}\left(\mathrm{1}^{\mathrm{2}} \right)+\frac{{x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)}{\mathrm{3}!}\left(\mathrm{1}^{\mathrm{3}} \right)+......+\mathrm{1}\:=\:\mathrm{4}{x} \\ $$$${ignore}\:{the}\:{continuity}\:\left({what}\:{rule}\:{is}\:.....\:{ignore}\:{the}\:+...+\right)\:{is}\:{it} \\ $$$${linear}\:{approximation} \\ $$$$\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} −{x}}{\mathrm{2}×\mathrm{1}}+\frac{\left({x}^{\mathrm{2}} −{x}\right)\left({x}−\mathrm{2}\right)}{\mathrm{3}×\mathrm{2}×\mathrm{1}}+\mathrm{1}\:=\:\mathrm{4}{x} \\ $$$$\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} −{x}}{\mathrm{2}}+\frac{{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{2}{x}}{\mathrm{6}}+\mathrm{1}\:=\:\mathrm{4}{x} \\ $$$$\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} −{x}}{\mathrm{2}}+\frac{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}}{\mathrm{6}}+\mathrm{1}\:=\:\mathrm{4}{x} \\ $$$${Multiply}\:{through}\:{by}\:\mathrm{6}\: \\ $$$$\mathrm{6}+\mathrm{6}{x}+\mathrm{3}\left({x}^{\mathrm{2}} −{x}\right)+{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{6}\:=\:\mathrm{24}{x} \\ $$$$\mathrm{12}+\mathrm{6}{x}+\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}+{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{6}\:=\:\mathrm{24}{x} \\ $$$$\mathrm{12}+\mathrm{5}{x}+{x}^{\mathrm{3}} \:=\:\mathrm{24}{x} \\ $$$$\mathrm{12}+\mathrm{5}{x}+{x}^{\mathrm{3}} −\mathrm{24}{x}\:=\:\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{19}{x}+\mathrm{12}\:=\:\mathrm{0} \\ $$$${Factorize} \\ $$$${x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}−\mathrm{3}{x}+\mathrm{12}\:=\:\mathrm{0} \\ $$$$\left({x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} \right)+\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}\right)−\left(\mathrm{3}{x}+\mathrm{12}\right)\:=\:\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left({x}−\mathrm{4}\right)+\mathrm{4}{x}\left({x}−\mathrm{4}\right)−\mathrm{3}\left({x}−\mathrm{4}\right)\:=\:\mathrm{0} \\ $$$${Factor}\:{out}\:\left({x}−\mathrm{4}\right) \\ $$$$\left({x}−\mathrm{4}\right)\left({x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{3}\right)\:=\:\mathrm{0} \\ $$$${x}−\mathrm{4}\:=\:\mathrm{0}\:{or}\:{x}^{\:\mathrm{2}} +\mathrm{4}{x}−\mathrm{3}\:=\:\mathrm{0} \\ $$$${x}\:=\:\mathrm{4}\:{or}\:{x}\:=\:\mathrm{0}.\mathrm{6458}\:{or}\:{x}\:=\:−\mathrm{4}.\mathrm{6458} \\ $$$${The}\:{only}\:{real}\:{solution}\:{is}\:{x}\:=\:\mathrm{4} \\ $$$${Therefore} \\ $$$${x}\:=\:\mathrm{4} \\ $$$$ \\ $$$${DONE}! \\ $$$$ \\ $$$${Please}\:{confirm}\:{the}\:{solution}.\:{is}\:{it}\:{correct}\:{or}\:{please}\:{corect}\:{it}\:{or} \\ $$$${show}\:{me}\:{alternative}. \\ $$$${This}\:{is}\:{my}\:{trial}. \\ $$$${Thanks}. \\ $$$$ \\ $$$$ \\ $$

Commented by prakash jain last updated on 26/May/16

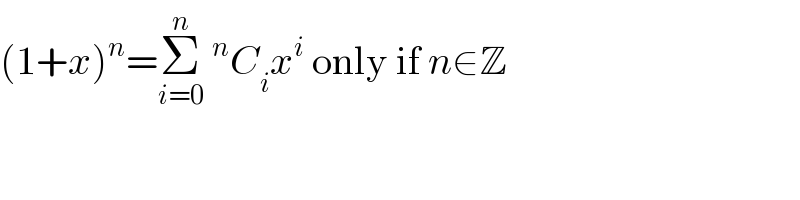
(1+x)^n =Σ_(i=0) ^n ^n C_i x^i only if n∈Z

$$\left(\mathrm{1}+{x}\right)^{{n}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\:^{{n}} {C}_{{i}} {x}^{{i}} \:\mathrm{only}\:\mathrm{if}\:{n}\in\mathbb{Z} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com