Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 211943 by Frix last updated on 25/Sep/24

2^(m−1) =1+mn m, n ∈Z

$$\mathrm{2}^{{m}−\mathrm{1}} =\mathrm{1}+{mn} \\ $$$${m},\:{n}\:\in\mathbb{Z} \\ $$

Commented by BHOOPENDRA last updated on 25/Sep/24

{(m,n)∈Z×Z ∣ m is odd &n=((2^(m−1) −1)/m)} Example of solutions .m=1,n=0 .m=3,n=1 .m=7,n=9 The integer solution (m,n) for both equation exist only when m is odd integer that is not a multiple of 3 .specially ,for value of m that are multiples of P(prime)(Except 1) (i.e,m=P(2k+1) where k∈Z^+ ), P ≥3there are no integer solutions for n.

$$\left\{\left({m},{n}\right)\in\mathbb{Z}×\mathbb{Z}\:\mid\:{m}\:{is}\:{odd}\:\&{n}=\frac{\mathrm{2}^{{m}−\mathrm{1}} −\mathrm{1}}{{m}}\right\} \\ $$$${Example}\:{of}\:{solutions} \\ $$$$.{m}=\mathrm{1},{n}=\mathrm{0} \\ $$$$.{m}=\mathrm{3},{n}=\mathrm{1} \\ $$$$.{m}=\mathrm{7},{n}=\mathrm{9} \\ $$$${The}\:{integer}\:{solution}\:\left({m},{n}\right)\:{for} \\ $$$${both}\:{equation}\:{exist}\:{only}\:{when}\:{m}\:{is}\: \\ $$$${odd}\:{integer}\:{that}\:{is}\:{not}\:{a}\:{multiple}\:{of} \\ $$$$\mathrm{3}\:.{specially}\:,{for}\:{value}\:{of}\:\boldsymbol{{m}}\:{that}\:{are} \\ $$$${multiples}\:{of}\:\mathbb{P}\left({prime}\right)\left({Except}\:\mathrm{1}\right) \\ $$$$\left({i}.{e},{m}=\mathbb{P}\left(\mathrm{2}{k}+\mathrm{1}\right)\:{where}\:{k}\in\mathbb{Z}^{+} \right), \\ $$$$\mathbb{P}\:\geq\mathrm{3}{there}\:{are}\:{no}\:{integer}\:{solutions}\:{for}\:{n}. \\ $$$$ \\ $$

Answered by BHOOPENDRA last updated on 25/Sep/24

{(m,n)∈Z×Z ∣m is odd and n=((2^(m−1) −1)/m)} for all odd value of m ∈Z^+ But for values of m that are odd multiple of P(prime) (i.e m=P(2k+1) where k∈ Z^+ & k≥1 ) there is no integer solutions for n except 1. N={m∈Z^+ :m=P(2k+1),k∈Z,k≥1,P≥3} The n=((2^(m−1) −1)/(m )) for odd m. 1. 2^(m−1) =1+mn 2. 2^(m−1) =1−mn Previous results Recape (for Equation 1)S_1 .m=1 ,n=0 m=3 n=1 m=5 ,n=3 m=7 ,n=9 m=9 ,no solution(n=28.3333) m=15 no solution m=11 n=93 m=13 n=315 m=15 no solution m=17 n=3855 m=21 no solution m=25 no solution m=27 no solution m=33 no solution similarly for equation 2 S_2 ={(1,0),(3,−1),(5,−3),(11,−93).....} Key Insight m=p(2k+1) for P≥3 ,k≥1 there are no solutions for n (Except 1)

$$\left\{\left({m},{n}\right)\in\mathbb{Z}×\mathbb{Z}\:\mid{m}\:{is}\:{odd}\:{and}\:{n}=\frac{\mathrm{2}^{{m}−\mathrm{1}} −\mathrm{1}}{{m}}\right\} \\ $$$${for}\:{all}\:{odd}\:{value}\:{of}\:{m}\:\in\mathbb{Z}^{+} \\ $$$${But}\:{for}\:{values}\:{of}\:\boldsymbol{{m}}\:\boldsymbol{{that}}\:\boldsymbol{{are}}\:\boldsymbol{{odd}} \\ $$$$\boldsymbol{{multiple}}\:\boldsymbol{{of}}\:\mathbb{P}\left({prime}\right) \\ $$$$\left(\boldsymbol{{i}}.\boldsymbol{{e}}\:\boldsymbol{{m}}=\mathbb{P}\left(\mathrm{2}\boldsymbol{{k}}+\mathrm{1}\right)\:\boldsymbol{{where}}\right. \\ $$$$\left.\boldsymbol{{k}}\in\:\mathbb{Z}^{+} \&\:{k}\geqslant\mathrm{1}\:\right)\:{there}\:{is}\:{no}\:{integer}\:{solutions}\: \\ $$$${for}\:{n}\:{except}\:\mathrm{1}. \\ $$$$\boldsymbol{{N}}=\left\{{m}\in\mathbb{Z}^{+} :{m}=\mathbb{P}\left(\mathrm{2}{k}+\mathrm{1}\right),{k}\in\mathbb{Z},{k}\geqslant\mathrm{1},\mathbb{P}\geqslant\mathrm{3}\right\} \\ $$$${The}\:{n}=\frac{\mathrm{2}^{{m}−\mathrm{1}} −\mathrm{1}}{{m}\:}\:{for}\:{odd}\:{m}. \\ $$$$\mathrm{1}.\:\mathrm{2}^{{m}−\mathrm{1}} =\mathrm{1}+{mn} \\ $$$$\mathrm{2}.\:\mathrm{2}^{{m}−\mathrm{1}} =\mathrm{1}−{mn} \\ $$$$\boldsymbol{{Previous}}\:\boldsymbol{{results}}\:\boldsymbol{{Recape}} \\ $$$$\left({for}\:{Equation}\:\mathrm{1}\right){S}_{\mathrm{1}} \\ $$$$.{m}=\mathrm{1}\:,{n}=\mathrm{0} \\ $$$${m}=\mathrm{3}\:{n}=\mathrm{1} \\ $$$${m}=\mathrm{5}\:,{n}=\mathrm{3} \\ $$$${m}=\mathrm{7}\:,{n}=\mathrm{9} \\ $$$${m}=\mathrm{9}\:,\boldsymbol{{no}}\:\boldsymbol{{solution}}\left(\boldsymbol{{n}}=\mathrm{28}.\mathrm{3333}\right) \\ $$$${m}=\mathrm{15}\:{no}\:{solution}\: \\ $$$${m}=\mathrm{11}\:{n}=\mathrm{93} \\ $$$${m}=\mathrm{13}\:{n}=\mathrm{315} \\ $$$${m}=\mathrm{15}\:{no}\:{solution} \\ $$$${m}=\mathrm{17}\:{n}=\mathrm{3855} \\ $$$${m}=\mathrm{21}\:{no}\:{solution}\: \\ $$$${m}=\mathrm{25}\:{no}\:{solution} \\ $$$${m}=\mathrm{27}\:{no}\:{solution}\: \\ $$$${m}=\mathrm{33}\:{no}\:{solution}\: \\ $$$${similarly}\:{for}\:{equation}\:\mathrm{2} \\ $$$${S}_{\mathrm{2}} =\left\{\left(\mathrm{1},\mathrm{0}\right),\left(\mathrm{3},−\mathrm{1}\right),\left(\mathrm{5},−\mathrm{3}\right),\left(\mathrm{11},−\mathrm{93}\right).....\right\} \\ $$$${Key}\:{Insight} \\ $$$${m}={p}\left(\mathrm{2}{k}+\mathrm{1}\right)\:{for}\:\mathbb{P}\geqslant\mathrm{3}\:,{k}\geqslant\mathrm{1}\:{there}\:{are} \\ $$$${no}\:{solutions}\:{for}\:{n}\:\left({Except}\:\mathrm{1}\right) \\ $$$$ \\ $$

Commented by Frix last updated on 25/Sep/24

m=9 ⇒ n=((85)/3) Check it again!

$${m}=\mathrm{9}\:\Rightarrow\:{n}=\frac{\mathrm{85}}{\mathrm{3}} \\ $$$$\mathrm{Check}\:\mathrm{it}\:\mathrm{again}! \\ $$

Commented by Frix last updated on 25/Sep/24

I first thought I made a mistake because you got all odd m... I′ve been in a hurry, sorry for that.

$$\mathrm{I}\:\mathrm{first}\:\mathrm{thought}\:\mathrm{I}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{because} \\ $$$$\mathrm{you}\:\mathrm{got}\:\mathrm{all}\:\mathrm{odd}\:{m}...\:\mathrm{I}'\mathrm{ve}\:\mathrm{been}\:\mathrm{in}\:\mathrm{a}\:\mathrm{hurry}, \\ $$$$\mathrm{sorry}\:\mathrm{for}\:\mathrm{that}. \\ $$

Commented by BHOOPENDRA last updated on 25/Sep/24

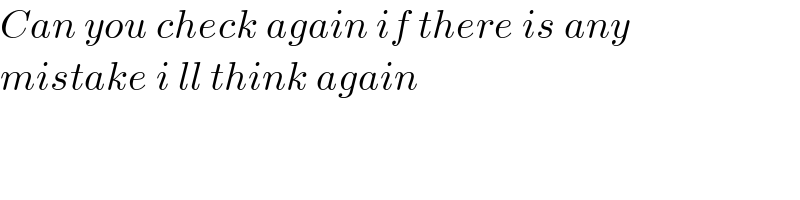
Can you check again if there is any mistake i ll think again

$${Can}\:{you}\:{check}\:{again}\:{if}\:{there}\:{is}\:{any} \\ $$$${mistake}\:{i}\:{ll}\:{think}\:{again} \\ $$

Commented by Frix last updated on 25/Sep/24

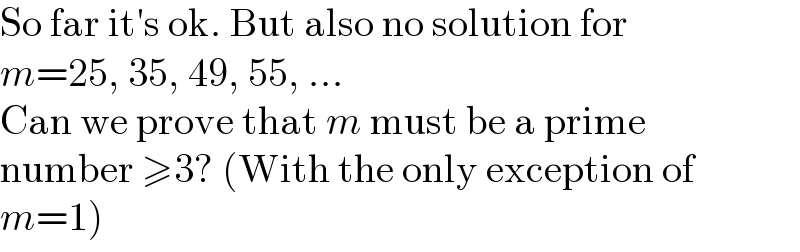
So far it′s ok. But also no solution for m=25, 35, 49, 55, ... Can we prove that m must be a prime number ≥3? (With the only exception of m=1)

$$\mathrm{So}\:\mathrm{far}\:\mathrm{it}'\mathrm{s}\:\mathrm{ok}.\:\mathrm{But}\:\mathrm{also}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{for} \\ $$$${m}=\mathrm{25},\:\mathrm{35},\:\mathrm{49},\:\mathrm{55},\:... \\ $$$$\mathrm{Can}\:\mathrm{we}\:\mathrm{prove}\:\mathrm{that}\:{m}\:\mathrm{must}\:\mathrm{be}\:\mathrm{a}\:\mathrm{prime} \\ $$$$\mathrm{number}\:\geqslant\mathrm{3}?\:\left(\mathrm{With}\:\mathrm{the}\:\mathrm{only}\:\mathrm{exception}\:\mathrm{of}\right. \\ $$$$\left.{m}=\mathrm{1}\right) \\ $$

Commented by A5T last updated on 25/Sep/24

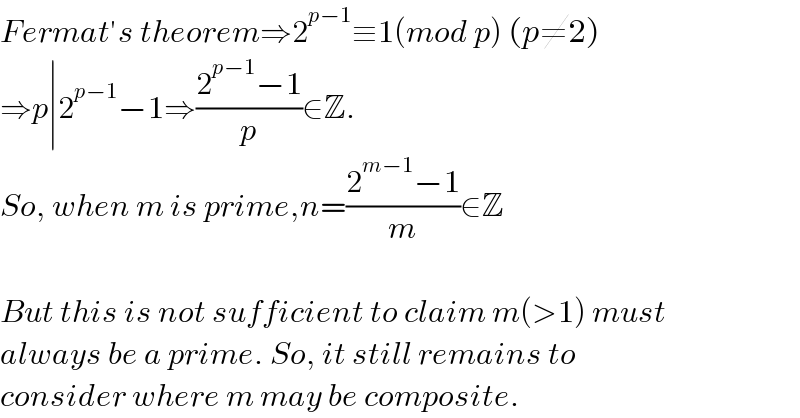
Fermat′s theorem⇒2^(p−1) ≡1(mod p) (p≠2) ⇒p∣2^(p−1) −1⇒((2^(p−1) −1)/p)∈Z. So, when m is prime,n=((2^(m−1) −1)/m)∈Z But this is not sufficient to claim m(>1) must always be a prime. So, it still remains to consider where m may be composite.

$${Fermat}'{s}\:{theorem}\Rightarrow\mathrm{2}^{{p}−\mathrm{1}} \equiv\mathrm{1}\left({mod}\:{p}\right)\:\left({p}\neq\mathrm{2}\right) \\ $$$$\Rightarrow{p}\mid\mathrm{2}^{{p}−\mathrm{1}} −\mathrm{1}\Rightarrow\frac{\mathrm{2}^{{p}−\mathrm{1}} −\mathrm{1}}{{p}}\in\mathbb{Z}. \\ $$$${So},\:{when}\:{m}\:{is}\:{prime},{n}=\frac{\mathrm{2}^{{m}−\mathrm{1}} −\mathrm{1}}{{m}}\in\mathbb{Z} \\ $$$$ \\ $$$${But}\:{this}\:{is}\:{not}\:{sufficient}\:{to}\:{claim}\:{m}\left(>\mathrm{1}\right)\:{must} \\ $$$${always}\:{be}\:{a}\:{prime}.\:{So},\:{it}\:{still}\:{remains}\:{to} \\ $$$${consider}\:{where}\:{m}\:{may}\:{be}\:{composite}. \\ $$

Commented by BHOOPENDRA last updated on 25/Sep/24

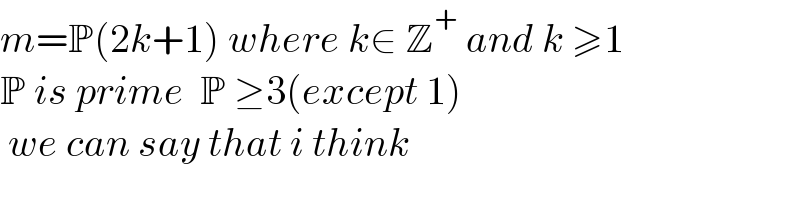
m=P(2k+1) where k∈ Z^+ and k ≥1 P is prime P ≥3(except 1) we can say that i think

$${m}=\mathbb{P}\left(\mathrm{2}{k}+\mathrm{1}\right)\:{where}\:{k}\in\:\mathbb{Z}^{+} \:{and}\:{k}\:\geqslant\mathrm{1}\: \\ $$$$\mathbb{P}\:{is}\:{prime}\:\:\mathbb{P}\:\geq\mathrm{3}\left({except}\:\mathrm{1}\right) \\ $$$$\:{we}\:{can}\:{say}\:{that}\:{i}\:{think} \\ $$

Answered by A5T last updated on 25/Sep/24

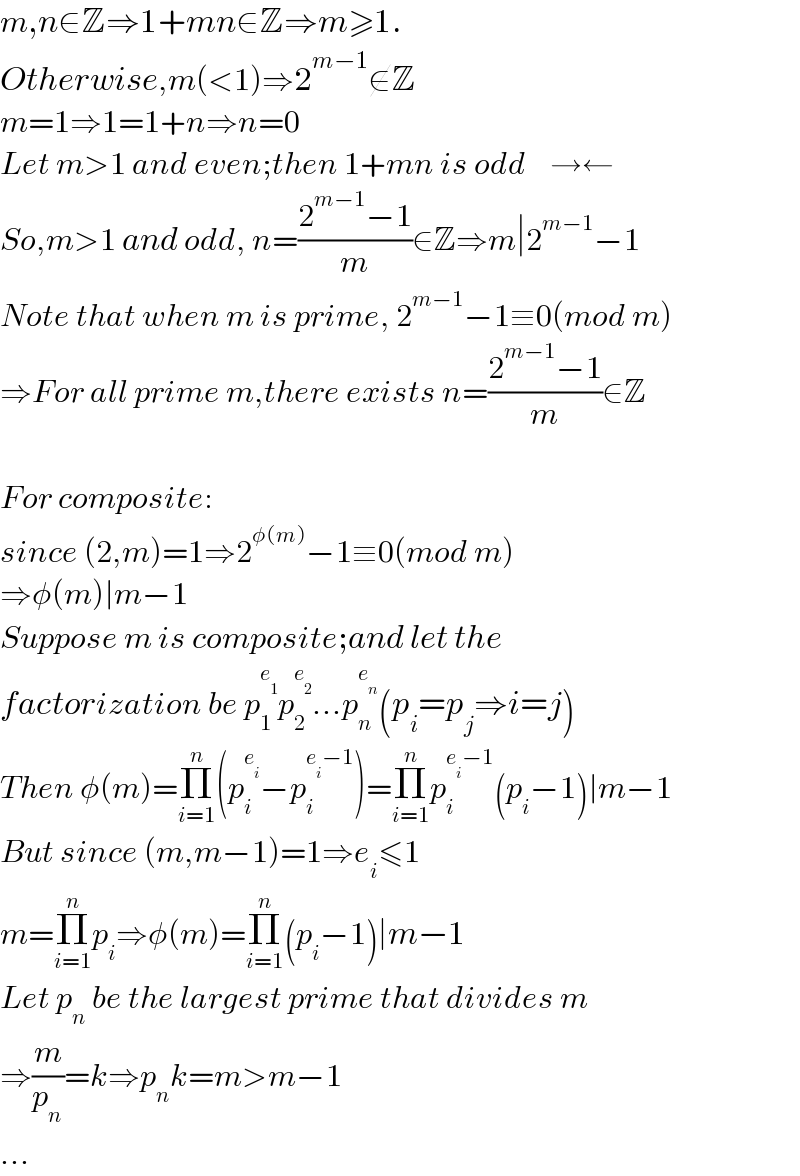
m,n∈Z⇒1+mn∈Z⇒m≥1. Otherwise,m(<1)⇒2^(m−1) ∉Z m=1⇒1=1+n⇒n=0 Let m>1 and even;then 1+mn is odd →← So,m>1 and odd, n=((2^(m−1) −1)/m)∈Z⇒m∣2^(m−1) −1 Note that when m is prime, 2^(m−1) −1≡0(mod m) ⇒For all prime m,there exists n=((2^(m−1) −1)/m)∈Z For composite: since (2,m)=1⇒2^(φ(m)) −1≡0(mod m) ⇒φ(m)∣m−1 Suppose m is composite;and let the factorization be p_1 ^e_1 p_2 ^e_2 ...p_n ^e_n (p_i =p_j ⇒i=j) Then φ(m)=Π_(i=1) ^n (p_i ^e_i −p_i ^(e_i −1) )=Π_(i=1) ^n p_i ^(e_i −1) (p_i −1)∣m−1 But since (m,m−1)=1⇒e_i ≤1 m=Π_(i=1) ^n p_i ⇒φ(m)=Π_(i=1) ^n (p_i −1)∣m−1 Let p_n be the largest prime that divides m ⇒(m/p_n )=k⇒p_n k=m>m−1 ...

$${m},{n}\in\mathbb{Z}\Rightarrow\mathrm{1}+{mn}\in\mathbb{Z}\Rightarrow{m}\geqslant\mathrm{1}. \\ $$$${Otherwise},{m}\left(<\mathrm{1}\right)\Rightarrow\mathrm{2}^{{m}−\mathrm{1}} \notin\mathbb{Z} \\ $$$${m}=\mathrm{1}\Rightarrow\mathrm{1}=\mathrm{1}+{n}\Rightarrow{n}=\mathrm{0} \\ $$$${Let}\:{m}>\mathrm{1}\:{and}\:{even};{then}\:\mathrm{1}+{mn}\:{is}\:{odd}\:\:\:\:\rightarrow\leftarrow \\ $$$${So},{m}>\mathrm{1}\:{and}\:{odd},\:{n}=\frac{\mathrm{2}^{{m}−\mathrm{1}} −\mathrm{1}}{{m}}\in\mathbb{Z}\Rightarrow{m}\mid\mathrm{2}^{{m}−\mathrm{1}} −\mathrm{1} \\ $$$${Note}\:{that}\:{when}\:{m}\:{is}\:{prime},\:\mathrm{2}^{{m}−\mathrm{1}} −\mathrm{1}\equiv\mathrm{0}\left({mod}\:{m}\right) \\ $$$$\Rightarrow{For}\:{all}\:{prime}\:{m},{there}\:{exists}\:{n}=\frac{\mathrm{2}^{{m}−\mathrm{1}} −\mathrm{1}}{{m}}\in\mathbb{Z} \\ $$$$ \\ $$$${For}\:{composite}: \\ $$$${since}\:\left(\mathrm{2},{m}\right)=\mathrm{1}\Rightarrow\mathrm{2}^{\phi\left({m}\right)} −\mathrm{1}\equiv\mathrm{0}\left({mod}\:{m}\right) \\ $$$$\Rightarrow\phi\left({m}\right)\mid{m}−\mathrm{1} \\ $$$${Suppose}\:{m}\:{is}\:{composite};{and}\:{let}\:{the}\: \\ $$$${factorization}\:{be}\:{p}_{\mathrm{1}} ^{{e}_{\mathrm{1}} } {p}_{\mathrm{2}} ^{{e}_{\mathrm{2}} } ...{p}_{{n}} ^{{e}_{{n}} } \left({p}_{{i}} ={p}_{{j}} \Rightarrow{i}={j}\right) \\ $$$${Then}\:\phi\left({m}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\left({p}_{{i}} ^{{e}_{{i}} } −{p}_{{i}} ^{{e}_{{i}} −\mathrm{1}} \right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{i}} ^{{e}_{{i}} −\mathrm{1}} \left({p}_{{i}} −\mathrm{1}\right)\mid{m}−\mathrm{1} \\ $$$${But}\:{since}\:\left({m},{m}−\mathrm{1}\right)=\mathrm{1}\Rightarrow{e}_{{i}} \leqslant\mathrm{1} \\ $$$${m}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{i}} \Rightarrow\phi\left({m}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\left({p}_{{i}} −\mathrm{1}\right)\mid{m}−\mathrm{1} \\ $$$${Let}\:{p}_{{n}} \:{be}\:{the}\:{largest}\:{prime}\:{that}\:{divides}\:{m} \\ $$$$\Rightarrow\frac{{m}}{{p}_{{n}} }={k}\Rightarrow{p}_{{n}} {k}={m}>{m}−\mathrm{1} \\ $$$$... \\ $$

Commented by A5T last updated on 25/Sep/24

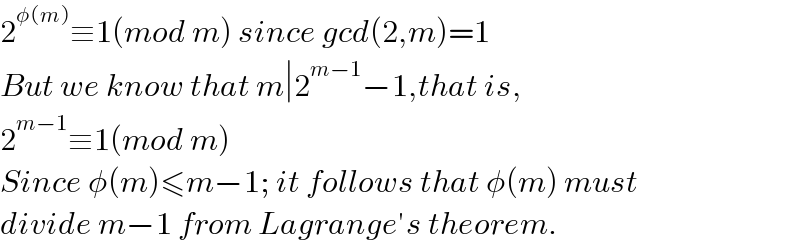
2^(φ(m)) ≡1(mod m) since gcd(2,m)=1 But we know that m∣2^(m−1) −1,that is, 2^(m−1) ≡1(mod m) Since φ(m)≤m−1; it follows that φ(m) must divide m−1 from Lagrange′s theorem.

$$\mathrm{2}^{\phi\left({m}\right)} \equiv\mathrm{1}\left({mod}\:{m}\right)\:{since}\:{gcd}\left(\mathrm{2},{m}\right)=\mathrm{1} \\ $$$${But}\:{we}\:{know}\:{that}\:{m}\mid\mathrm{2}^{{m}−\mathrm{1}} −\mathrm{1},{that}\:{is}, \\ $$$$\mathrm{2}^{{m}−\mathrm{1}} \equiv\mathrm{1}\left({mod}\:{m}\right) \\ $$$${Since}\:\phi\left({m}\right)\leqslant{m}−\mathrm{1};\:{it}\:{follows}\:{that}\:\phi\left({m}\right)\:{must} \\ $$$${divide}\:{m}−\mathrm{1}\:{from}\:{Lagrange}'{s}\:{theorem}. \\ $$

Commented by BHOOPENDRA last updated on 25/Sep/24

The key point is to recheck the assumption that φ(m)∣m−1 for composite m. This is not true in general ,and thus ,the reasoning for the composite case breakdown .while fermat′s Little theorem for prime,Euler′s theorem does not gaurantee that m∣2^(m−1 ) for composite m,beacuse φ(m) does not necessarily divide (m−1) To correct the reasoning,we would need to carefully anlyze specific composite number where m∣2^(m−1) holds ,without relying on φ(m)∣m−1 as a genral rule.

$${The}\:{key}\:{point}\:{is}\:{to}\:{recheck}\:{the}\:{assumption} \\ $$$${that}\:\phi\left({m}\right)\mid{m}−\mathrm{1}\:{for}\:{composite}\:{m}. \\ $$$${This}\:{is}\:{not}\:{true}\:{in}\:{general}\:,{and}\:{thus} \\ $$$$,{the}\:{reasoning}\:{for}\:{the}\:{composite}\:{case} \\ $$$${breakdown}\:.{while}\:{fermat}'{s}\:{Little}\:{theorem} \\ $$$${for}\:{prime},{Euler}'{s}\:{theorem}\:{does}\:{not} \\ $$$${gaurantee}\:{that}\:{m}\mid\mathrm{2}^{{m}−\mathrm{1}\:} {for}\:{composite} \\ $$$${m},{beacuse}\:\phi\left({m}\right)\:{does}\:{not}\:{necessarily} \\ $$$${divide}\:\left({m}−\mathrm{1}\right) \\ $$$${To}\:{correct}\:{the}\:{reasoning},{we}\:{would}\:{need} \\ $$$${to}\:{carefully}\:{anlyze}\:{specific}\:{composite} \\ $$$${number}\:{where}\:{m}\mid\mathrm{2}^{{m}−\mathrm{1}} {holds}\:,{without} \\ $$$${relying}\:{on}\:\phi\left({m}\right)\mid{m}−\mathrm{1}\:{as}\:{a}\:{genral}\:{rule}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com