Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 197171 by MM42 last updated on 09/Sep/23

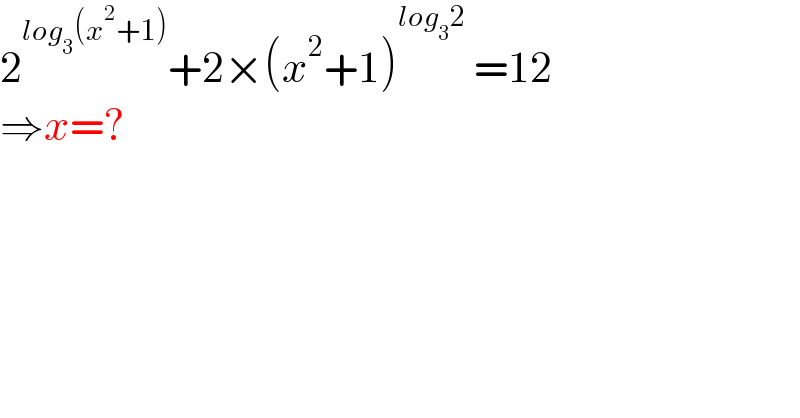
2^(log_3 (x^2 +1)) +2×(x^2 +1)^(log_3 2) =12 ⇒x=?

$$\mathrm{2}^{{log}_{\mathrm{3}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)} +\mathrm{2}×\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{log}_{\mathrm{3}} \mathrm{2}} \:=\mathrm{12} \\ $$$$\Rightarrow{x}=? \\ $$$$ \\ $$

Answered by Frix last updated on 09/Sep/23

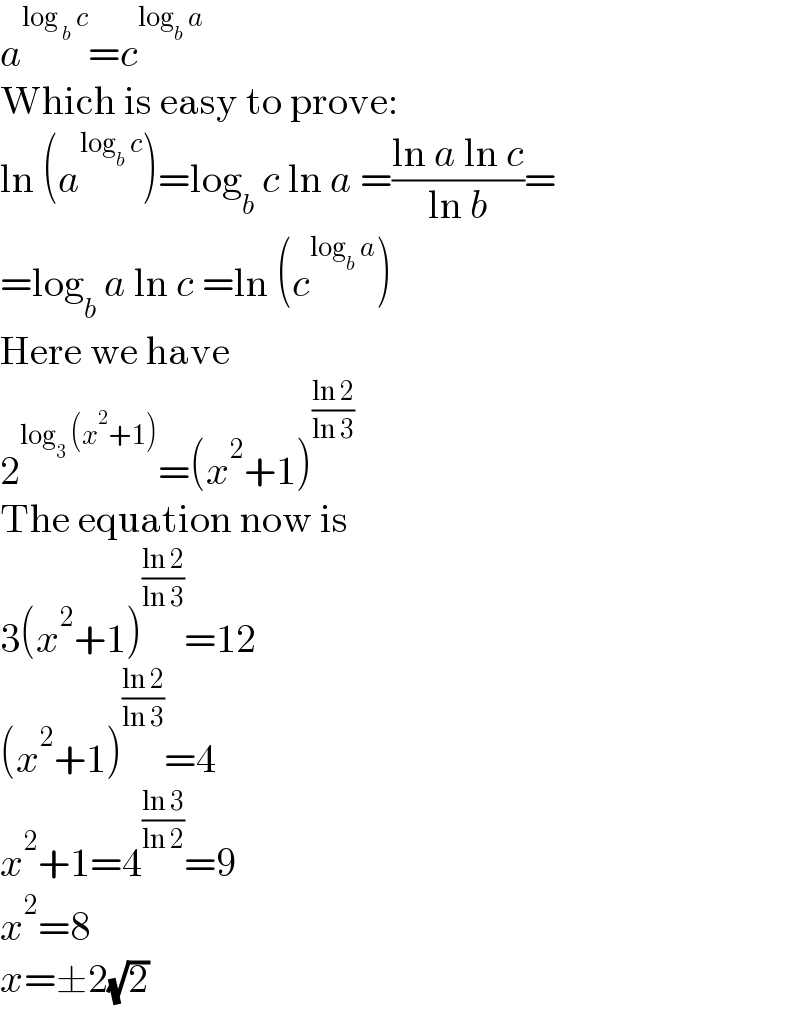
a^(log_( b) c) =c^(log_b a) Which is easy to prove: ln (a^(log_b c) )=log_b c ln a =((ln a ln c)/(ln b))= =log_b a ln c =ln (c^(log_b a) ) Here we have 2^(log_3 (x^2 +1)) =(x^2 +1)^((ln 2)/(ln 3)) The equation now is 3(x^2 +1)^((ln 2)/(ln 3)) =12 (x^2 +1)^((ln 2)/(ln 3)) =4 x^2 +1=4^((ln 3)/(ln 2)) =9 x^2 =8 x=±2(√2)

$${a}^{\mathrm{log}_{\:{b}} \:{c}} ={c}^{\mathrm{log}_{{b}} \:{a}} \\ $$$$\mathrm{Which}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{prove}: \\ $$$$\mathrm{ln}\:\left({a}^{\mathrm{log}_{{b}} \:{c}} \right)=\mathrm{log}_{{b}} \:{c}\:\mathrm{ln}\:{a}\:=\frac{\mathrm{ln}\:{a}\:\mathrm{ln}\:{c}}{\mathrm{ln}\:{b}}= \\ $$$$=\mathrm{log}_{{b}} \:{a}\:\mathrm{ln}\:{c}\:=\mathrm{ln}\:\left({c}^{\mathrm{log}_{{b}} \:{a}} \right) \\ $$$$\mathrm{Here}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{2}^{\mathrm{log}_{\mathrm{3}} \:\left({x}^{\mathrm{2}} +\mathrm{1}\right)} =\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{3}}} \\ $$$$\mathrm{The}\:\mathrm{equation}\:\mathrm{now}\:\mathrm{is} \\ $$$$\mathrm{3}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{3}}} =\mathrm{12} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{3}}} =\mathrm{4} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}=\mathrm{4}^{\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}} =\mathrm{9} \\ $$$${x}^{\mathrm{2}} =\mathrm{8} \\ $$$${x}=\pm\mathrm{2}\sqrt{\mathrm{2}} \\ $$

Commented by MM42 last updated on 10/Sep/23

very good . ⋛

$${very}\:\:{good}\:.\:\:\:\cancel{\lesseqgtr} \\ $$

Commented by Frix last updated on 10/Sep/23

��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com