Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 191663 by mathlove last updated on 28/Apr/23

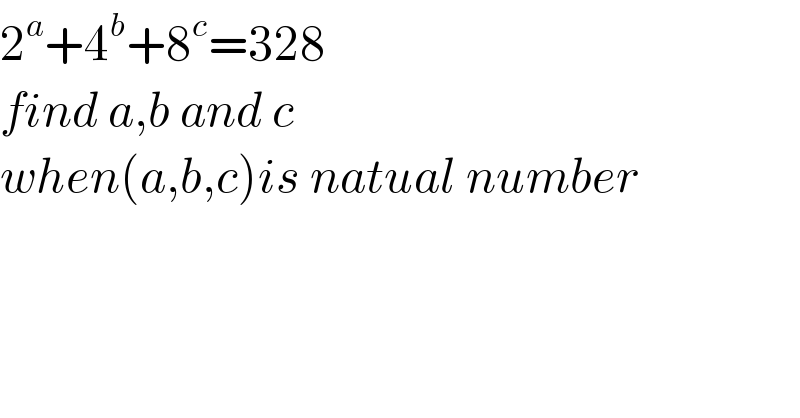
2^a +4^b +8^c =328 find a,b and c when(a,b,c)is natual number

$$\mathrm{2}^{{a}} +\mathrm{4}^{{b}} +\mathrm{8}^{{c}} =\mathrm{328} \\ $$$${find}\:{a},{b}\:{and}\:{c} \\ $$$${when}\left({a},{b},{c}\right){is}\:{natual}\:{number} \\ $$

Answered by Rasheed.Sindhi last updated on 28/Apr/23

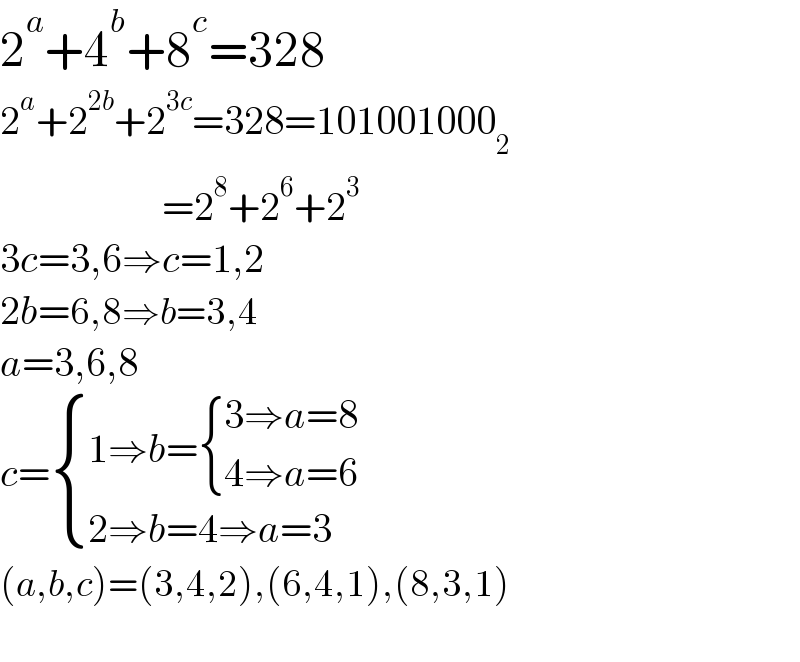
2^a +4^b +8^c =328 2^a +2^(2b) +2^(3c) =328=101001000_2 =2^8 +2^6 +2^3 3c=3,6⇒c=1,2 2b=6,8⇒b=3,4 a=3,6,8 c= { ((1⇒b= { ((3⇒a=8)),((4⇒a=6)) :})),((2⇒b=4⇒a=3)) :} (a,b,c)=(3,4,2),(6,4,1),(8,3,1)

$$\mathrm{2}^{{a}} +\mathrm{4}^{{b}} +\mathrm{8}^{{c}} =\mathrm{328} \\ $$$$\mathrm{2}^{{a}} +\mathrm{2}^{\mathrm{2}{b}} +\mathrm{2}^{\mathrm{3}{c}} =\mathrm{328}=\mathrm{101001000}_{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{8}} +\mathrm{2}^{\mathrm{6}} +\mathrm{2}^{\mathrm{3}} \\ $$$$\mathrm{3}{c}=\mathrm{3},\mathrm{6}\Rightarrow{c}=\mathrm{1},\mathrm{2} \\ $$$$\mathrm{2}{b}=\mathrm{6},\mathrm{8}\Rightarrow{b}=\mathrm{3},\mathrm{4} \\ $$$${a}=\mathrm{3},\mathrm{6},\mathrm{8} \\ $$$${c}=\begin{cases}{\mathrm{1}\Rightarrow{b}=\begin{cases}{\mathrm{3}\Rightarrow{a}=\mathrm{8}}\\{\mathrm{4}\Rightarrow{a}=\mathrm{6}}\end{cases}}\\{\mathrm{2}\Rightarrow{b}=\mathrm{4}\Rightarrow{a}=\mathrm{3}}\end{cases} \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{4},\mathrm{2}\right),\left(\mathrm{6},\mathrm{4},\mathrm{1}\right),\left(\mathrm{8},\mathrm{3},\mathrm{1}\right) \\ $$$$ \\ $$

Commented by BaliramKumar last updated on 28/Apr/23

Nice solution Sir

$$\mathrm{Nice}\:\mathrm{solution}\:\mathrm{Sir} \\ $$

Commented by mathlove last updated on 28/Apr/23

thanks sir

$${thanks}\:{sir} \\ $$

Answered by BaliramKumar last updated on 28/Apr/23

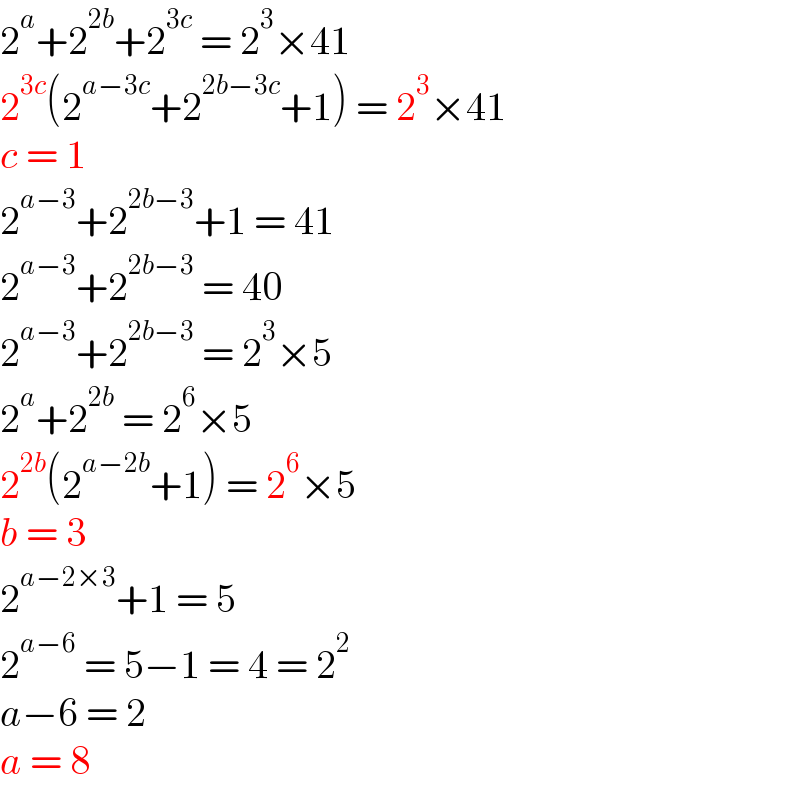
2^a +2^(2b) +2^(3c) = 2^3 ×41 2^(3c) (2^(a−3c) +2^(2b−3c) +1) = 2^3 ×41 c = 1 2^(a−3) +2^(2b−3) +1 = 41 2^(a−3) +2^(2b−3) = 40 2^(a−3) +2^(2b−3) = 2^3 ×5 2^a +2^(2b) = 2^6 ×5 2^(2b) (2^(a−2b) +1) = 2^6 ×5 b = 3 2^(a−2×3) +1 = 5 2^(a−6) = 5−1 = 4 = 2^2 a−6 = 2 a = 8

$$\mathrm{2}^{{a}} +\mathrm{2}^{\mathrm{2}{b}} +\mathrm{2}^{\mathrm{3}{c}} \:=\:\mathrm{2}^{\mathrm{3}} ×\mathrm{41} \\ $$$$\mathrm{2}^{\mathrm{3}{c}} \left(\mathrm{2}^{{a}−\mathrm{3}{c}} +\mathrm{2}^{\mathrm{2}{b}−\mathrm{3}{c}} +\mathrm{1}\right)\:=\:\mathrm{2}^{\mathrm{3}} ×\mathrm{41} \\ $$$${c}\:=\:\mathrm{1} \\ $$$$\mathrm{2}^{{a}−\mathrm{3}} +\mathrm{2}^{\mathrm{2}{b}−\mathrm{3}} +\mathrm{1}\:=\:\mathrm{41} \\ $$$$\mathrm{2}^{{a}−\mathrm{3}} +\mathrm{2}^{\mathrm{2}{b}−\mathrm{3}} \:=\:\mathrm{40} \\ $$$$\mathrm{2}^{{a}−\mathrm{3}} +\mathrm{2}^{\mathrm{2}{b}−\mathrm{3}} \:=\:\mathrm{2}^{\mathrm{3}} ×\mathrm{5} \\ $$$$\mathrm{2}^{{a}} +\mathrm{2}^{\mathrm{2}{b}} \:=\:\mathrm{2}^{\mathrm{6}} ×\mathrm{5} \\ $$$$\mathrm{2}^{\mathrm{2}{b}} \left(\mathrm{2}^{{a}−\mathrm{2}{b}} +\mathrm{1}\right)\:=\:\mathrm{2}^{\mathrm{6}} ×\mathrm{5} \\ $$$${b}\:=\:\mathrm{3} \\ $$$$\mathrm{2}^{{a}−\mathrm{2}×\mathrm{3}} +\mathrm{1}\:=\:\mathrm{5} \\ $$$$\mathrm{2}^{{a}−\mathrm{6}} \:=\:\mathrm{5}−\mathrm{1}\:=\:\mathrm{4}\:=\:\mathrm{2}^{\mathrm{2}} \\ $$$${a}−\mathrm{6}\:=\:\mathrm{2} \\ $$$${a}\:=\:\mathrm{8} \\ $$

Commented by mathlove last updated on 28/Apr/23

thanks

$${thanks} \\ $$

Answered by mehdee42 last updated on 28/Apr/23

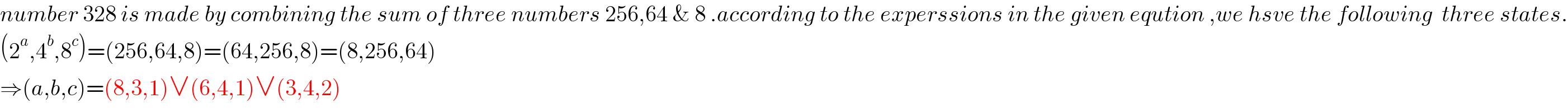
number 328 is made by combining the sum of three numbers 256,64 & 8 .according to the experssions in the given eqution ,we hsve the following three states. (2^a ,4^b ,8^c )=(256,64,8)=(64,256,8)=(8,256,64) ⇒(a,b,c)=(8,3,1)∨(6,4,1)∨(3,4,2)

$${number}\:\mathrm{328}\:{is}\:{made}\:{by}\:{combining}\:{the}\:{sum}\:{of}\:{three}\:{numbers}\:\mathrm{256},\mathrm{64}\:\&\:\mathrm{8}\:.{according}\:{to}\:{the}\:{experssions}\:{in}\:{the}\:{given}\:{eqution}\:,{we}\:{hsve}\:{the}\:{following}\:\:{three}\:{states}. \\ $$$$\left(\mathrm{2}^{{a}} ,\mathrm{4}^{{b}} ,\mathrm{8}^{{c}} \right)=\left(\mathrm{256},\mathrm{64},\mathrm{8}\right)=\left(\mathrm{64},\mathrm{256},\mathrm{8}\right)=\left(\mathrm{8},\mathrm{256},\mathrm{64}\right) \\ $$$$\Rightarrow\left({a},{b},{c}\right)=\left(\mathrm{8},\mathrm{3},\mathrm{1}\right)\vee\left(\mathrm{6},\mathrm{4},\mathrm{1}\right)\vee\left(\mathrm{3},\mathrm{4},\mathrm{2}\right)\: \\ $$

Answered by LOSER last updated on 29/Apr/23

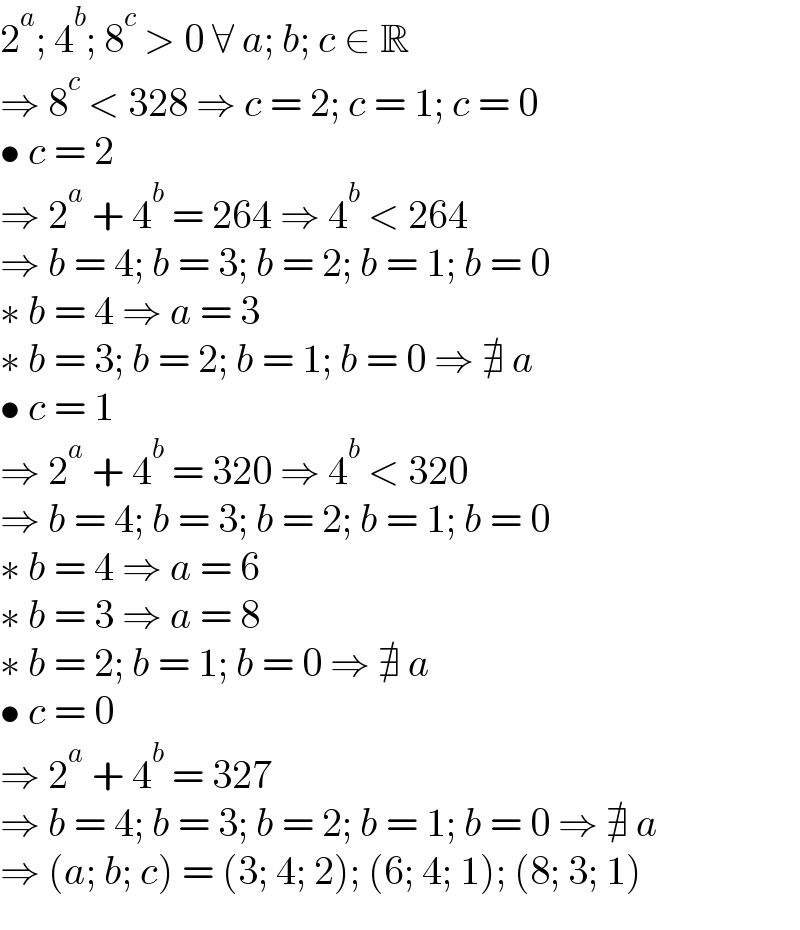
2^a ; 4^b ; 8^c > 0 ∀ a; b; c ∈ R ⇒ 8^c < 328 ⇒ c = 2; c = 1; c = 0 • c = 2 ⇒ 2^a + 4^b = 264 ⇒ 4^b < 264 ⇒ b = 4; b = 3; b = 2; b = 1; b = 0 ∗ b = 4 ⇒ a = 3 ∗ b = 3; b = 2; b = 1; b = 0 ⇒ ∄ a • c = 1 ⇒ 2^a + 4^b = 320 ⇒ 4^b < 320 ⇒ b = 4; b = 3; b = 2; b = 1; b = 0 ∗ b = 4 ⇒ a = 6 ∗ b = 3 ⇒ a = 8 ∗ b = 2; b = 1; b = 0 ⇒ ∄ a • c = 0 ⇒ 2^a + 4^b = 327 ⇒ b = 4; b = 3; b = 2; b = 1; b = 0 ⇒ ∄ a ⇒ (a; b; c) = (3; 4; 2); (6; 4; 1); (8; 3; 1)

$$\mathrm{2}^{{a}} ;\:\mathrm{4}^{{b}} ;\:\mathrm{8}^{{c}} \:>\:\mathrm{0}\:\forall\:{a};\:{b};\:{c}\:\in\:\mathbb{R} \\ $$$$\Rightarrow\:\mathrm{8}^{{c}} \:<\:\mathrm{328}\:\Rightarrow\:{c}\:=\:\mathrm{2};\:{c}\:=\:\mathrm{1};\:{c}\:=\:\mathrm{0} \\ $$$$\bullet\:{c}\:=\:\mathrm{2}\: \\ $$$$\Rightarrow\:\mathrm{2}^{{a}} \:+\:\mathrm{4}^{{b}} \:=\:\mathrm{264}\:\Rightarrow\:\mathrm{4}^{{b}} \:<\:\mathrm{264} \\ $$$$\Rightarrow\:{b}\:=\:\mathrm{4};\:{b}\:=\:\mathrm{3};\:{b}\:=\:\mathrm{2};\:{b}\:=\:\mathrm{1};\:{b}\:=\:\mathrm{0} \\ $$$$\ast\:{b}\:=\:\mathrm{4}\:\Rightarrow\:{a}\:=\:\mathrm{3} \\ $$$$\ast\:{b}\:=\:\mathrm{3};\:{b}\:=\:\mathrm{2};\:{b}\:=\:\mathrm{1};\:{b}\:=\:\mathrm{0}\:\Rightarrow\:\nexists\:{a} \\ $$$$\bullet\:{c}\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{2}^{{a}} \:+\:\mathrm{4}^{{b}} \:=\:\mathrm{320}\:\Rightarrow\:\mathrm{4}^{{b}} \:<\:\mathrm{320} \\ $$$$\Rightarrow\:{b}\:=\:\mathrm{4};\:{b}\:=\:\mathrm{3};\:{b}\:=\:\mathrm{2};\:{b}\:=\:\mathrm{1};\:{b}\:=\:\mathrm{0} \\ $$$$\ast\:{b}\:=\:\mathrm{4}\:\Rightarrow\:{a}\:=\:\mathrm{6} \\ $$$$\ast\:{b}\:=\:\mathrm{3}\:\Rightarrow\:{a}\:=\:\mathrm{8} \\ $$$$\ast\:{b}\:=\:\mathrm{2};\:{b}\:=\:\mathrm{1};\:{b}\:=\:\mathrm{0}\:\Rightarrow\:\nexists\:{a} \\ $$$$\bullet\:{c}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2}^{{a}} \:+\:\mathrm{4}^{{b}} \:=\:\mathrm{327} \\ $$$$\Rightarrow\:{b}\:=\:\mathrm{4};\:{b}\:=\:\mathrm{3};\:{b}\:=\:\mathrm{2};\:{b}\:=\:\mathrm{1};\:{b}\:=\:\mathrm{0}\:\Rightarrow\:\nexists\:{a} \\ $$$$\Rightarrow\:\left({a};\:{b};\:{c}\right)\:=\:\left(\mathrm{3};\:\mathrm{4};\:\mathrm{2}\right);\:\left(\mathrm{6};\:\mathrm{4};\:\mathrm{1}\right);\:\left(\mathrm{8};\:\mathrm{3};\:\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com