
Question Number 178165 by Spillover last updated on 13/Oct/22

$$\mathrm{2}.\mathrm{86g}\:\mathrm{of}\:\mathrm{hydrated}\:\mathrm{Sodium}\:\mathrm{carbonate} \\ $$$$\boldsymbol{\mathrm{Na}}_{\mathrm{2}} \boldsymbol{\mathrm{CO}}_{\mathrm{3}} .\boldsymbol{\mathrm{nH}}_{\mathrm{2}} \boldsymbol{\mathrm{O}}\:\mathrm{was}\:\mathrm{dissolved} \\ $$$$\mathrm{into}\:\mathrm{water}\:\mathrm{to}\:\mathrm{make}\:\mathrm{250cm}^{\mathrm{3}} \:\mathrm{solution} \\ $$$$\mathrm{of}\:\:\mathrm{0}.\mathrm{04M}\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{n} \\ $$
Answered by a.lgnaoui last updated on 14/Oct/22
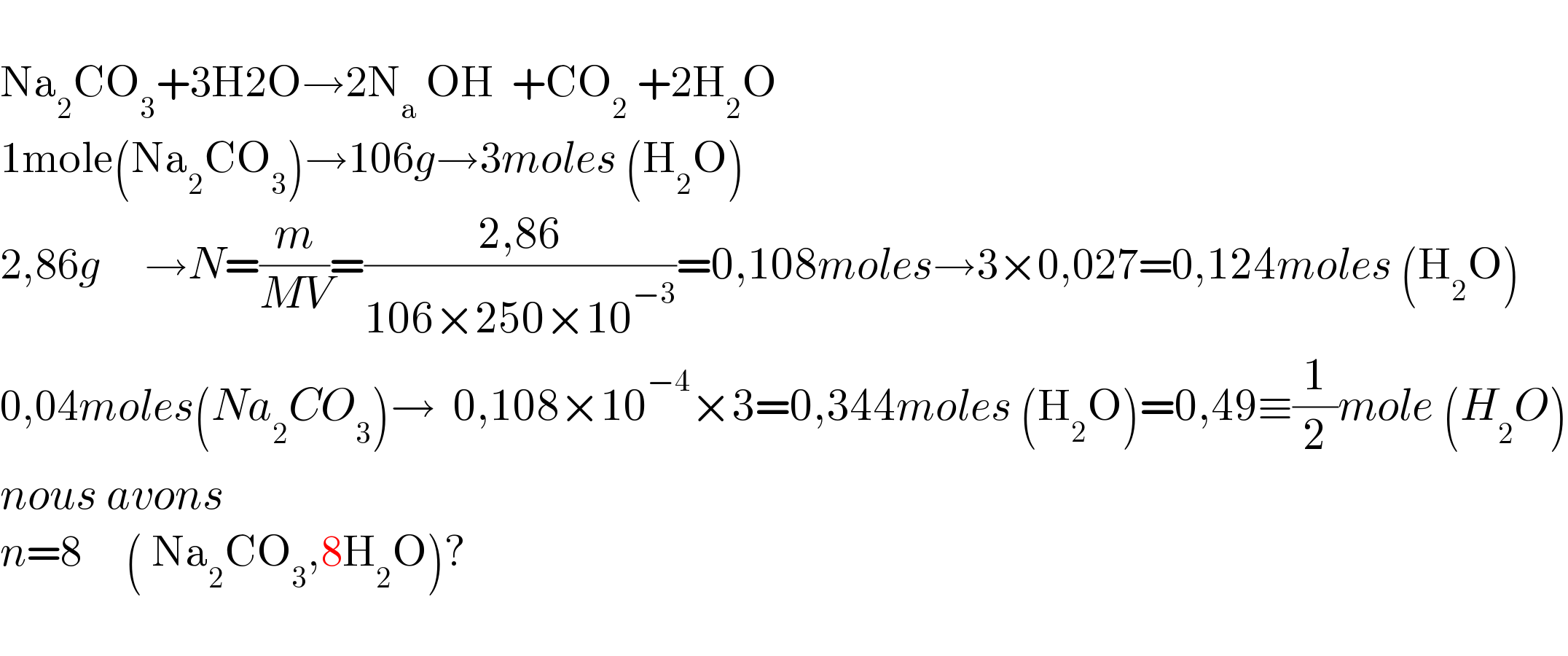
$$ \\ $$$$\mathrm{Na}_{\mathrm{2}} \mathrm{CO}_{\mathrm{3}} +\mathrm{3H2O}\rightarrow\mathrm{2N}_{\mathrm{a}} \:\mathrm{OH}\:\:+\mathrm{CO}_{\mathrm{2}} \:+\mathrm{2H}_{\mathrm{2}} \mathrm{O} \\ $$$$\mathrm{1mole}\left(\mathrm{Na}_{\mathrm{2}} \mathrm{CO}_{\mathrm{3}} \right)\rightarrow\mathrm{106}{g}\rightarrow\mathrm{3}{moles}\:\left(\mathrm{H}_{\mathrm{2}} \mathrm{O}\right) \\ $$$$\mathrm{2},\mathrm{86}{g}\:\:\:\:\:\rightarrow{N}=\frac{{m}}{{MV}}=\frac{\mathrm{2},\mathrm{86}}{\mathrm{106}×\mathrm{250}×\mathrm{10}^{−\mathrm{3}} }=\mathrm{0},\mathrm{108}{moles}\rightarrow\mathrm{3}×\mathrm{0},\mathrm{027}=\mathrm{0},\mathrm{124}{moles}\:\left(\mathrm{H}_{\mathrm{2}} \mathrm{O}\right) \\ $$$$\mathrm{0},\mathrm{04}{moles}\left({Na}_{\mathrm{2}} {CO}_{\mathrm{3}} \right)\rightarrow\:\:\mathrm{0},\mathrm{108}×\mathrm{10}^{−\mathrm{4}} ×\mathrm{3}=\mathrm{0},\mathrm{344}{moles}\:\left(\mathrm{H}_{\mathrm{2}} \mathrm{O}\right)=\mathrm{0},\mathrm{49}\equiv\frac{\mathrm{1}}{\mathrm{2}}{mole}\:\left({H}_{\mathrm{2}} {O}\right) \\ $$$${nous}\:{avons}\:\: \\ $$$${n}=\mathrm{8}\:\:\:\:\:\left(\:\mathrm{Na}_{\mathrm{2}} \mathrm{CO}_{\mathrm{3}} ,\mathrm{8H}_{\mathrm{2}} \mathrm{O}\right)? \\ $$$$ \\ $$
Commented by Spillover last updated on 14/Oct/22

$$\mathrm{n}=\mathrm{10} \\ $$
Answered by Spillover last updated on 14/Oct/22
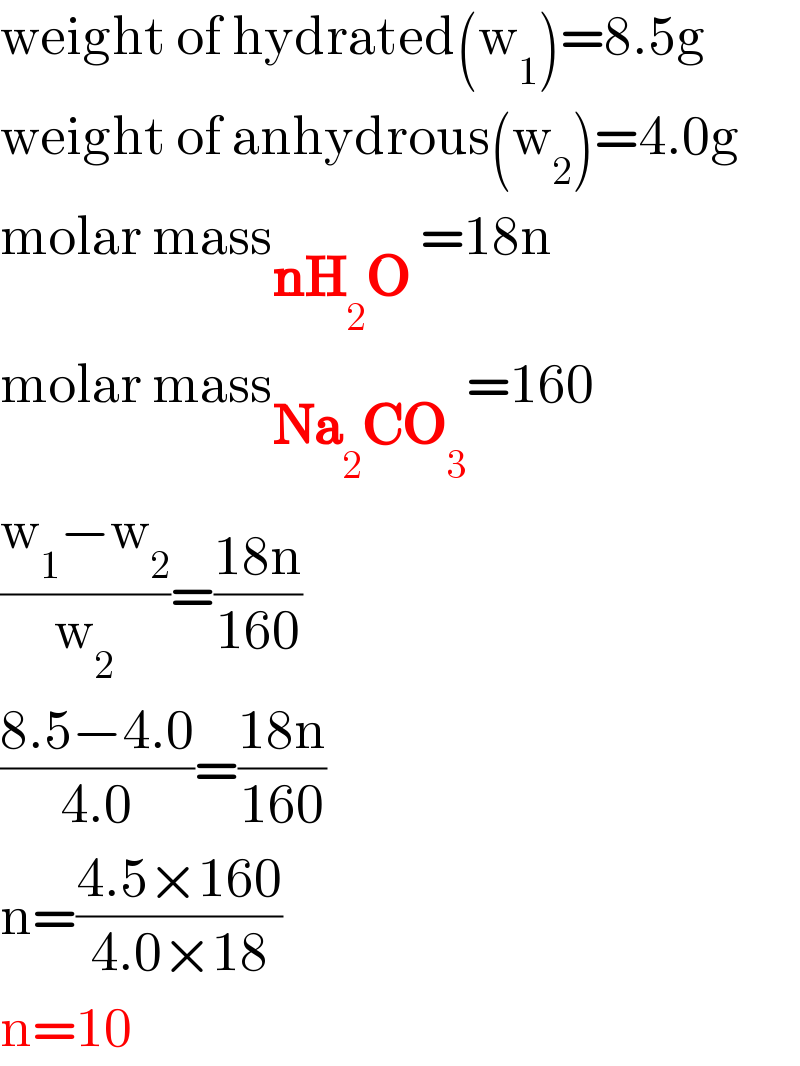
$$\mathrm{weight}\:\mathrm{of}\:\mathrm{hydrated}\left(\mathrm{w}_{\mathrm{1}} \right)=\mathrm{8}.\mathrm{5g} \\ $$$$\mathrm{weight}\:\mathrm{of}\:\mathrm{anhydrous}\left(\mathrm{w}_{\mathrm{2}} \right)=\mathrm{4}.\mathrm{0g} \\ $$$$\mathrm{molar}\:\mathrm{mass}_{\boldsymbol{\mathrm{nH}}_{\mathrm{2}} \boldsymbol{\mathrm{O}}\:} =\mathrm{18n} \\ $$$$\mathrm{molar}\:\mathrm{mass}_{\boldsymbol{\mathrm{Na}}_{\mathrm{2}} \boldsymbol{\mathrm{CO}}_{\mathrm{3}} } =\mathrm{160} \\ $$$$\frac{\mathrm{w}_{\mathrm{1}} −\mathrm{w}_{\mathrm{2}} }{\mathrm{w}_{\mathrm{2}} }=\frac{\mathrm{18n}}{\mathrm{160}} \\ $$$$\frac{\mathrm{8}.\mathrm{5}−\mathrm{4}.\mathrm{0}}{\mathrm{4}.\mathrm{0}}=\frac{\mathrm{18n}}{\mathrm{160}} \\ $$$$\mathrm{n}=\frac{\mathrm{4}.\mathrm{5}×\mathrm{160}}{\mathrm{4}.\mathrm{0}×\mathrm{18}} \\ $$$$\mathrm{n}=\mathrm{10} \\ $$
