
Question Number 17759 by chux last updated on 10/Jul/17
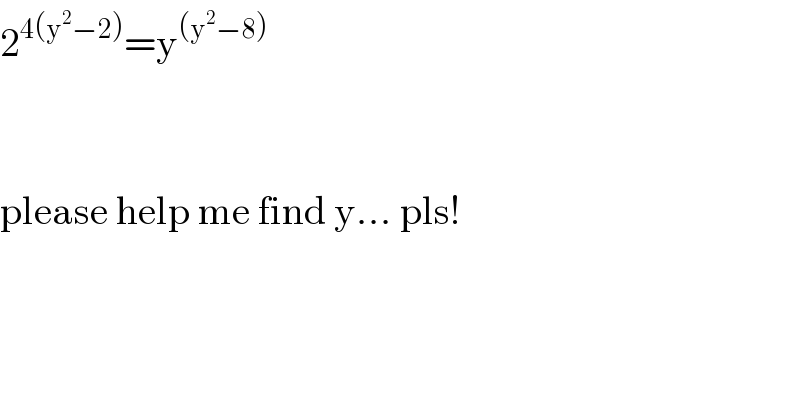
$$\mathrm{2}^{\mathrm{4}\left(\mathrm{y}^{\mathrm{2}} −\mathrm{2}\right)} =\mathrm{y}^{\left(\mathrm{y}^{\mathrm{2}} −\mathrm{8}\right)} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{find}\:\mathrm{y}...\:\mathrm{pls}! \\ $$
Answered by mrW1 last updated on 10/Jul/17
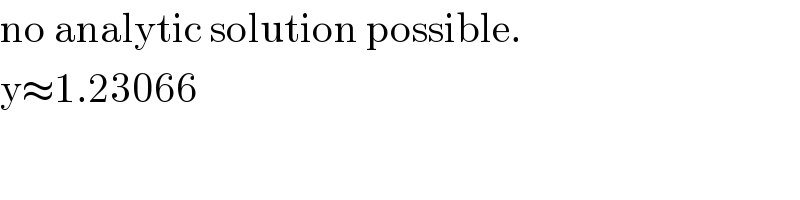
$$\mathrm{no}\:\mathrm{analytic}\:\mathrm{solution}\:\mathrm{possible}. \\ $$$$\mathrm{y}\approx\mathrm{1}.\mathrm{23066} \\ $$
Commented by chux last updated on 10/Jul/17
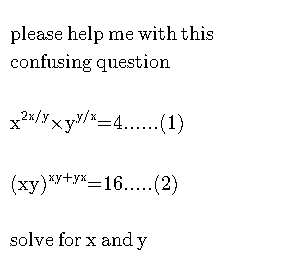
Commented by chux last updated on 10/Jul/17

$$\mathrm{when}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{your} \\ $$$$\mathrm{solution}\:\mathrm{to}\:\mathrm{this}\:\mathrm{question}\:\mathrm{i}\:\mathrm{arrived} \\ $$$$\mathrm{at}\:\mathrm{this}\:\mathrm{equation}......\:\mathrm{This}\:\mathrm{means}\: \\ $$$$\mathrm{that}\:\mathrm{i}\:\mathrm{did}\:\mathrm{not}\:\mathrm{really}\:\mathrm{understand} \\ $$$$\mathrm{your}\:\mathrm{approach}\:\mathrm{majorly}\:\mathrm{at}\:\mathrm{the} \\ $$$$\mathrm{end}\:\mathrm{of}\:\mathrm{the}\:\mathrm{solution}.\:\mathrm{I}\:\mathrm{ll}\:\mathrm{love}\:\mathrm{it}\:\mathrm{if} \\ $$$$\mathrm{you}\:\mathrm{shed}\:\mathrm{more}\:\mathrm{light}\:\mathrm{to}\:\mathrm{it}\:\mathrm{sir}. \\ $$$$ \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{always}\:\mathrm{assisting}. \\ $$
Commented by mrW1 last updated on 10/Jul/17
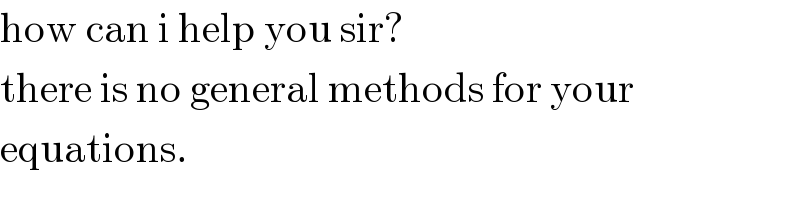
$$\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{help}\:\mathrm{you}\:\mathrm{sir}? \\ $$$$\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{general}\:\mathrm{methods}\:\mathrm{for}\:\mathrm{your} \\ $$$$\mathrm{equations}. \\ $$
Commented by chux last updated on 10/Jul/17

$$\mathrm{i}\:\mathrm{actually}\:\mathrm{understand}\:\mathrm{your}\:\mathrm{step} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{top}\:\mathrm{until}\:\mathrm{the}\:\mathrm{last}\:\mathrm{step} \\ $$$$\mathrm{before}\:\mathrm{you}\:\mathrm{got}\:\mathrm{x}=\mathrm{1} \\ $$$$ \\ $$$$\mathrm{x}^{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}/\mathrm{x}^{\mathrm{2}} \right)} =\mathrm{2}^{\mathrm{2}\left(\mathrm{1}−\mathrm{1}/\mathrm{x}^{\mathrm{2}} \right)} \\ $$$$ \\ $$$$\mathrm{x}=\mathrm{1}\:\mathrm{and}\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{i}\:\mathrm{dont}\:\mathrm{know}\:\mathrm{how}\:\mathrm{you}\:\mathrm{got}\:\mathrm{the}\:\mathrm{result} \\ $$$$\mathrm{x}=\mathrm{1} \\ $$
Commented by mrW1 last updated on 10/Jul/17

$$\mathrm{1}^{\mathrm{p}} =\mathrm{2}^{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{as}\:\mathrm{i}\:\mathrm{haved}\:\mathrm{said}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{general} \\ $$$$\mathrm{method}\:\mathrm{one}\:\mathrm{can}\:\mathrm{follow}\:\mathrm{blindly}.\:\mathrm{one} \\ $$$$\mathrm{has}\:\mathrm{to}\:\mathrm{try}\:\mathrm{and}\:\mathrm{see}\:\mathrm{if}\:\mathrm{error}. \\ $$
Commented by chux last updated on 10/Jul/17

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
