Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 53877 by Mikael_Marshall last updated on 26/Jan/19

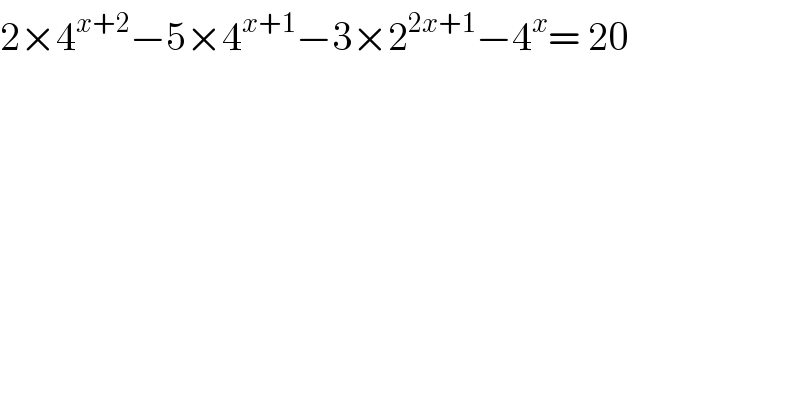
2×4^(x+2) −5×4^(x+1) −3×2^(2x+1) −4^x = 20

$$\mathrm{2}×\mathrm{4}^{{x}+\mathrm{2}} −\mathrm{5}×\mathrm{4}^{{x}+\mathrm{1}} −\mathrm{3}×\mathrm{2}^{\mathrm{2}{x}+\mathrm{1}} −\mathrm{4}^{{x}} =\:\mathrm{20} \\ $$

Commented by Abdo msup. last updated on 27/Jan/19

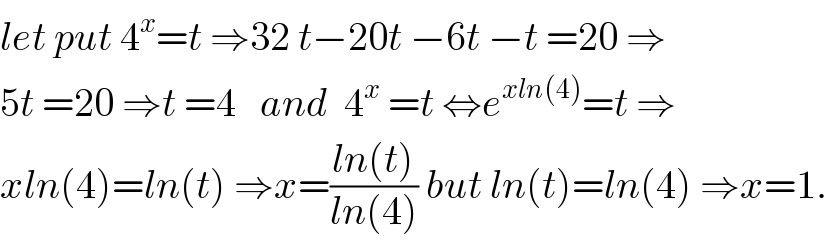
let put 4^x =t ⇒32 t−20t −6t −t =20 ⇒ 5t =20 ⇒t =4 and 4^x =t ⇔e^(xln(4)) =t ⇒ xln(4)=ln(t) ⇒x=((ln(t))/(ln(4))) but ln(t)=ln(4) ⇒x=1.

$${let}\:{put}\:\mathrm{4}^{{x}} ={t}\:\Rightarrow\mathrm{32}\:{t}−\mathrm{20}{t}\:−\mathrm{6}{t}\:−{t}\:=\mathrm{20}\:\Rightarrow \\ $$$$\mathrm{5}{t}\:=\mathrm{20}\:\Rightarrow{t}\:=\mathrm{4}\:\:\:{and}\:\:\mathrm{4}^{{x}} \:={t}\:\Leftrightarrow{e}^{{xln}\left(\mathrm{4}\right)} ={t}\:\Rightarrow \\ $$$${xln}\left(\mathrm{4}\right)={ln}\left({t}\right)\:\Rightarrow{x}=\frac{{ln}\left({t}\right)}{{ln}\left(\mathrm{4}\right)}\:{but}\:{ln}\left({t}\right)={ln}\left(\mathrm{4}\right)\:\Rightarrow{x}=\mathrm{1}. \\ $$

Answered by byaw last updated on 26/Jan/19

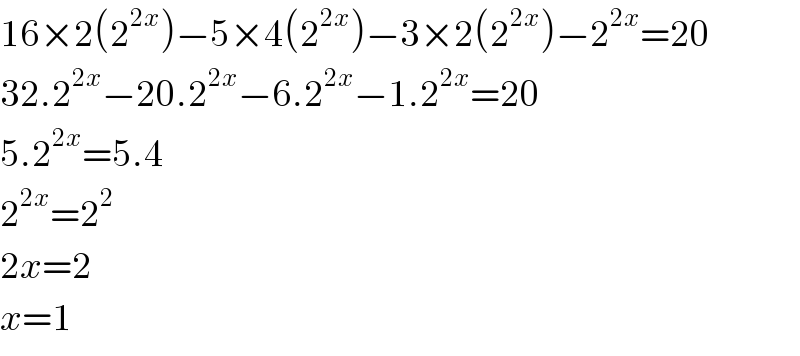
16×2(2^(2x) )−5×4(2^(2x) )−3×2(2^(2x) )−2^(2x) =20 32.2^(2x) −20.2^(2x) −6.2^(2x) −1.2^(2x) =20 5.2^(2x) =5.4 2^(2x) =2^2 2x=2 x=1

$$\mathrm{16}×\mathrm{2}\left(\mathrm{2}^{\mathrm{2}{x}} \right)−\mathrm{5}×\mathrm{4}\left(\mathrm{2}^{\mathrm{2}{x}} \right)−\mathrm{3}×\mathrm{2}\left(\mathrm{2}^{\mathrm{2}{x}} \right)−\mathrm{2}^{\mathrm{2}{x}} =\mathrm{20} \\ $$$$\mathrm{32}.\mathrm{2}^{\mathrm{2}{x}} −\mathrm{20}.\mathrm{2}^{\mathrm{2}{x}} −\mathrm{6}.\mathrm{2}^{\mathrm{2}{x}} −\mathrm{1}.\mathrm{2}^{\mathrm{2}{x}} =\mathrm{20} \\ $$$$\mathrm{5}.\mathrm{2}^{\mathrm{2}{x}} =\mathrm{5}.\mathrm{4} \\ $$$$\mathrm{2}^{\mathrm{2}{x}} =\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}=\mathrm{2} \\ $$$${x}=\mathrm{1} \\ $$

Commented by Mikael_Marshall last updated on 26/Jan/19

thanks Sir. I′m learning a lot.

$${thanks}\:{Sir}.\:{I}'{m}\:{learning}\:{a}\:{lot}. \\ $$

Answered by F_Nongue last updated on 26/Jan/19

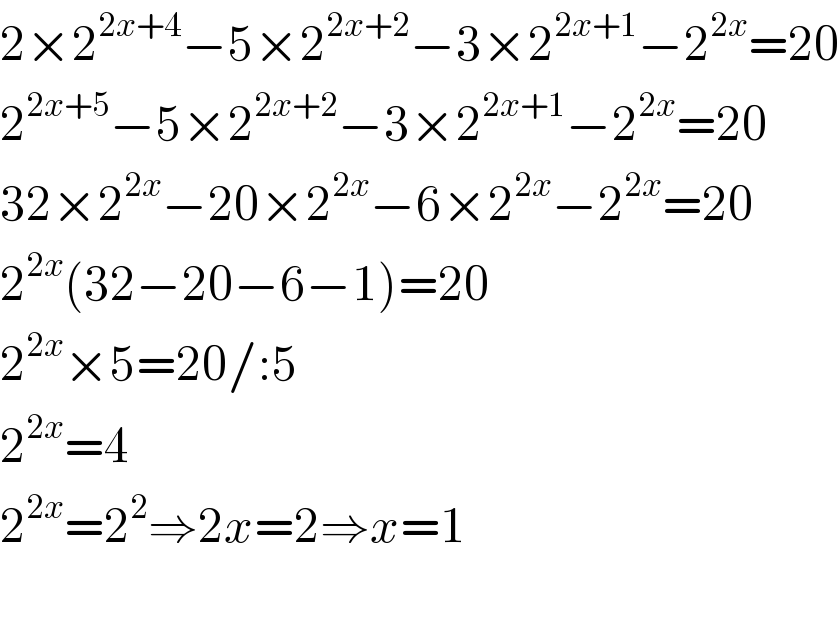
2×2^(2x+4) −5×2^(2x+2) −3×2^(2x+1) −2^(2x) =20 2^(2x+5) −5×2^(2x+2) −3×2^(2x+1) −2^(2x) =20 32×2^(2x) −20×2^(2x) −6×2^(2x) −2^(2x) =20 2^(2x) (32−20−6−1)=20 2^(2x) ×5=20/:5 2^(2x) =4 2^(2x) =2^2 ⇒2x=2⇒x=1

$$\mathrm{2}×\mathrm{2}^{\mathrm{2}{x}+\mathrm{4}} −\mathrm{5}×\mathrm{2}^{\mathrm{2}{x}+\mathrm{2}} −\mathrm{3}×\mathrm{2}^{\mathrm{2}{x}+\mathrm{1}} −\mathrm{2}^{\mathrm{2}{x}} =\mathrm{20} \\ $$$$\mathrm{2}^{\mathrm{2}{x}+\mathrm{5}} −\mathrm{5}×\mathrm{2}^{\mathrm{2}{x}+\mathrm{2}} −\mathrm{3}×\mathrm{2}^{\mathrm{2}{x}+\mathrm{1}} −\mathrm{2}^{\mathrm{2}{x}} =\mathrm{20} \\ $$$$\mathrm{32}×\mathrm{2}^{\mathrm{2}{x}} −\mathrm{20}×\mathrm{2}^{\mathrm{2}{x}} −\mathrm{6}×\mathrm{2}^{\mathrm{2}{x}} −\mathrm{2}^{\mathrm{2}{x}} =\mathrm{20} \\ $$$$\mathrm{2}^{\mathrm{2}{x}} \left(\mathrm{32}−\mathrm{20}−\mathrm{6}−\mathrm{1}\right)=\mathrm{20} \\ $$$$\mathrm{2}^{\mathrm{2}{x}} ×\mathrm{5}=\mathrm{20}/:\mathrm{5} \\ $$$$\mathrm{2}^{\mathrm{2}{x}} =\mathrm{4} \\ $$$$\mathrm{2}^{\mathrm{2}{x}} =\mathrm{2}^{\mathrm{2}} \Rightarrow\mathrm{2}{x}=\mathrm{2}\Rightarrow{x}=\mathrm{1} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com