Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 204957 by CrispyXYZ last updated on 03/Mar/24

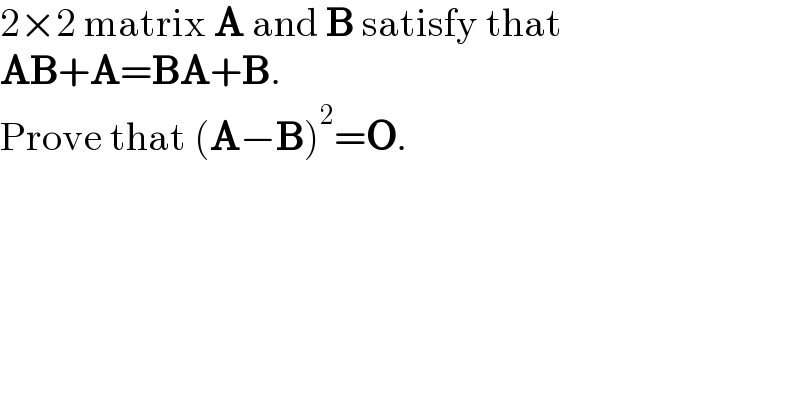
2×2 matrix A and B satisfy that AB+A=BA+B. Prove that (A−B)^2 =O.

$$\mathrm{2}×\mathrm{2}\:\mathrm{matrix}\:\boldsymbol{\mathrm{A}}\:\mathrm{and}\:\boldsymbol{\mathrm{B}}\:\mathrm{satisfy}\:\mathrm{that} \\ $$$$\boldsymbol{\mathrm{AB}}+\boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{BA}}+\boldsymbol{\mathrm{B}}. \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\left(\boldsymbol{\mathrm{A}}−\boldsymbol{\mathrm{B}}\right)^{\mathrm{2}} =\boldsymbol{\mathrm{O}}. \\ $$

Answered by Rajpurohith last updated on 04/Mar/24

Need not hold true! take A=−I and B=I satisfy the given condition yet (A−B)^2 ≠0

$${Need}\:{not}\:{hold}\:{true}! \\ $$$${take}\:{A}=−{I}\:{and}\:{B}={I}\:{satisfy}\:{the}\:{given}\:{condition} \\ $$$${yet}\:\left({A}−{B}\right)^{\mathrm{2}} \neq\mathrm{0} \\ $$

Commented by MM42 last updated on 04/Mar/24

−2I≠0

$$−\mathrm{2}{I}\neq\mathrm{0}\: \\ $$

Answered by witcher3 last updated on 04/Mar/24

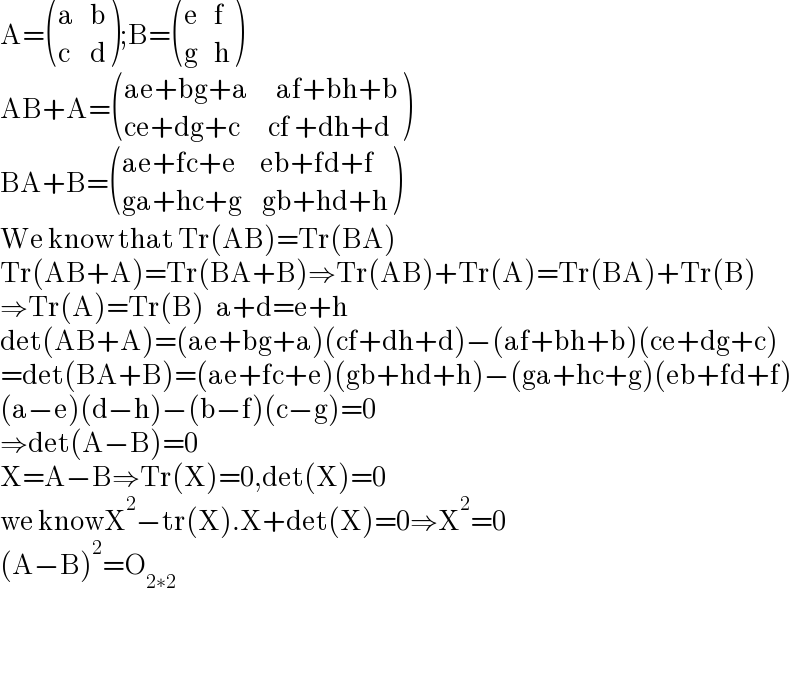
A= (((a b)),((c d)) );B= (((e f)),((g h)) ) AB+A= (((ae+bg+a af+bh+b)),((ce+dg+c cf +dh+d)) ) BA+B= (((ae+fc+e eb+fd+f)),((ga+hc+g gb+hd+h)) ) We know that Tr(AB)=Tr(BA) Tr(AB+A)=Tr(BA+B)⇒Tr(AB)+Tr(A)=Tr(BA)+Tr(B) ⇒Tr(A)=Tr(B) a+d=e+h det(AB+A)=(ae+bg+a)(cf+dh+d)−(af+bh+b)(ce+dg+c) =det(BA+B)=(ae+fc+e)(gb+hd+h)−(ga+hc+g)(eb+fd+f) (a−e)(d−h)−(b−f)(c−g)=0 ⇒det(A−B)=0 X=A−B⇒Tr(X)=0,det(X)=0 we knowX^2 −tr(X).X+det(X)=0⇒X^2 =0 (A−B)^2 =O_(2∗2)

$$\mathrm{A}=\begin{pmatrix}{\mathrm{a}\:\:\:\:\mathrm{b}}\\{\mathrm{c}\:\:\:\:\:\mathrm{d}}\end{pmatrix};\mathrm{B}=\begin{pmatrix}{\mathrm{e}\:\:\:\:\mathrm{f}}\\{\mathrm{g}\:\:\:\:\mathrm{h}}\end{pmatrix} \\ $$$$\mathrm{AB}+\mathrm{A}=\begin{pmatrix}{\mathrm{ae}+\mathrm{bg}+\mathrm{a}\:\:\:\:\:\:\:\mathrm{af}+\mathrm{bh}+\mathrm{b}}\\{\mathrm{ce}+\mathrm{dg}+\mathrm{c}\:\:\:\:\:\:\:\mathrm{cf}\:+\mathrm{dh}+\mathrm{d}}\end{pmatrix} \\ $$$$\mathrm{BA}+\mathrm{B}=\begin{pmatrix}{\mathrm{ae}+\mathrm{fc}+\mathrm{e}\:\:\:\:\:\:\mathrm{eb}+\mathrm{fd}+\mathrm{f}}\\{\mathrm{ga}+\mathrm{hc}+\mathrm{g}\:\:\:\:\:\mathrm{gb}+\mathrm{hd}+\mathrm{h}}\end{pmatrix} \\ $$$$\mathrm{We}\:\mathrm{know}\:\mathrm{that}\:\mathrm{Tr}\left(\mathrm{AB}\right)=\mathrm{Tr}\left(\mathrm{BA}\right) \\ $$$$\mathrm{Tr}\left(\mathrm{AB}+\mathrm{A}\right)=\mathrm{Tr}\left(\mathrm{BA}+\mathrm{B}\right)\Rightarrow\mathrm{Tr}\left(\mathrm{AB}\right)+\mathrm{Tr}\left(\mathrm{A}\right)=\mathrm{Tr}\left(\mathrm{BA}\right)+\mathrm{Tr}\left(\mathrm{B}\right) \\ $$$$\Rightarrow\mathrm{Tr}\left(\mathrm{A}\right)=\mathrm{Tr}\left(\mathrm{B}\right)\:\:\:\mathrm{a}+\mathrm{d}=\mathrm{e}+\mathrm{h} \\ $$$$\mathrm{det}\left(\mathrm{AB}+\mathrm{A}\right)=\left(\mathrm{ae}+\mathrm{bg}+\mathrm{a}\right)\left(\mathrm{cf}+\mathrm{dh}+\mathrm{d}\right)−\left(\mathrm{af}+\mathrm{bh}+\mathrm{b}\right)\left(\mathrm{ce}+\mathrm{dg}+\mathrm{c}\right) \\ $$$$=\mathrm{det}\left(\mathrm{BA}+\mathrm{B}\right)=\left(\mathrm{ae}+\mathrm{fc}+\mathrm{e}\right)\left(\mathrm{gb}+\mathrm{hd}+\mathrm{h}\right)−\left(\mathrm{ga}+\mathrm{hc}+\mathrm{g}\right)\left(\mathrm{eb}+\mathrm{fd}+\mathrm{f}\right) \\ $$$$\left(\mathrm{a}−\mathrm{e}\right)\left(\mathrm{d}−\mathrm{h}\right)−\left(\mathrm{b}−\mathrm{f}\right)\left(\mathrm{c}−\mathrm{g}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{det}\left(\mathrm{A}−\mathrm{B}\right)=\mathrm{0} \\ $$$$\mathrm{X}=\mathrm{A}−\mathrm{B}\Rightarrow\mathrm{Tr}\left(\mathrm{X}\right)=\mathrm{0},\mathrm{det}\left(\mathrm{X}\right)=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{knowX}^{\mathrm{2}} −\mathrm{tr}\left(\mathrm{X}\right).\mathrm{X}+\mathrm{det}\left(\mathrm{X}\right)=\mathrm{0}\Rightarrow\mathrm{X}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{A}−\mathrm{B}\right)^{\mathrm{2}} =\mathrm{O}_{\mathrm{2}\ast\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com