
Question Number 212231 by Davidtim last updated on 07/Oct/24
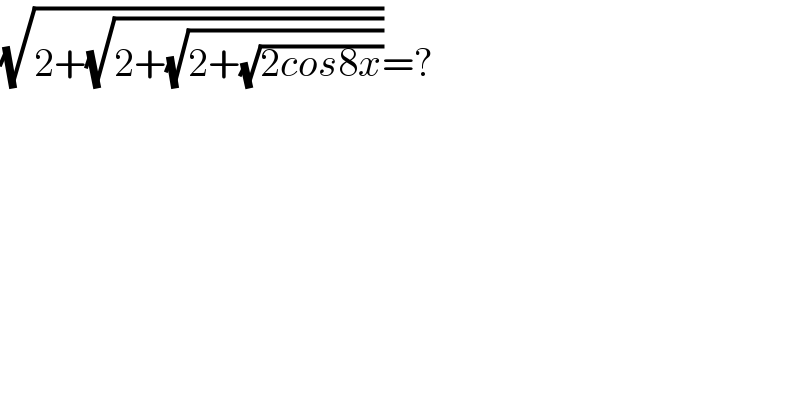
$$\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}{cos}\mathrm{8}{x}}}}}=? \\ $$
Commented by Davidtim last updated on 07/Oct/24

$${please}\:{help}\:{me} \\ $$
Commented by mr W last updated on 08/Oct/24

$${then}\:{at}\:{first}\:{you}\:{should}\:{help}\:{other} \\ $$$${people}\:{to}\:{understand}\:{what}\:{you}\:{want} \\ $$$${other}\:{people}\:{do}. \\ $$
Commented by Ghisom last updated on 08/Oct/24
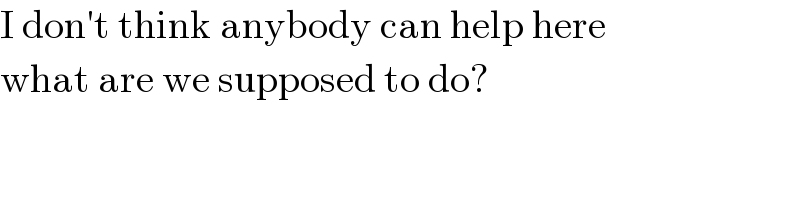
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{anybody}\:\mathrm{can}\:\mathrm{help}\:\mathrm{here} \\ $$$$\mathrm{what}\:\mathrm{are}\:\mathrm{we}\:\mathrm{supposed}\:\mathrm{to}\:\mathrm{do}? \\ $$
Commented by Davidtim last updated on 08/Oct/24
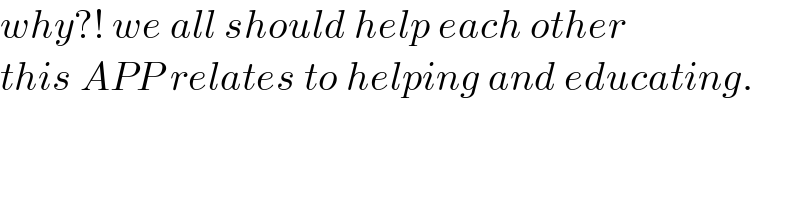
$${why}?!\:{we}\:{all}\:{should}\:{help}\:{each}\:{other} \\ $$$${this}\:{APP}\:{relates}\:{to}\:{helping}\:{and}\:{educating}. \\ $$
Commented by Davidtim last updated on 08/Oct/24

$$? \\ $$
Commented by Davidtim last updated on 08/Oct/24

$${If}\:{I}\:{cant}\:{solve}\:{the}\:{problem}\:{then}\:{need} \\ $$$${your}\:{help}. \\ $$
Commented by mr W last updated on 08/Oct/24

$${it}'{s}\:{not}\:{that}\:{they}\:{don}'{t}\:{help}\:{you},\:{but} \\ $$$${they}\:{don}'{t}\:{know}\:{what}\:{you}\:{expect}. \\ $$$${if}\:{you}\:{want}\:{to}\:{simply}\:{the}\:{expression}, \\ $$$${i}\:{think}\:{you}\:{can}\:{not}\:{simply}\:{it}\:{more}. \\ $$
Commented by Davidtim last updated on 08/Oct/24

$${Ok}\:{sir}\:{I}\:{have}\:{uploaded}\:{the}\:{problem} \\ $$$${and}\:{I}\:{have}\:{expected}\:{of}\:{solotion}\:{the}\:{problem}. \\ $$$${I}\:{mention}\:{again}\:{here}\:{please}\:{solve}\:{this}. \\ $$$$\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}{cos}\mathrm{8}{x}}}}}=? \\ $$
Commented by mr W last updated on 08/Oct/24
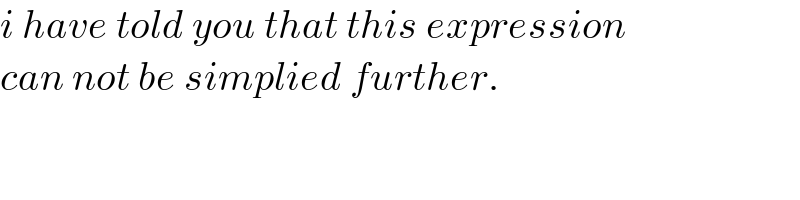
$${i}\:{have}\:{told}\:{you}\:{that}\:{this}\:{expression} \\ $$$${can}\:{not}\:{be}\:{simplied}\:{further}. \\ $$
Commented by Davidtim last updated on 08/Oct/24
$${ok}\:{sir}\:{thanks}\:{lots}\:{of}. \\ $$
Commented by TonyCWX08 last updated on 08/Oct/24
$${You}\:{guve}\:{us}\:{an}\:{expression}\:{and}\:{expect}\:{us}\:{to}\:{simplify}\:{it}?? \\ $$
Answered by ajfour last updated on 08/Oct/24
![(√(2+(√(2+(√(2+(√(2cos8x))))))))=q {(q^2 −2)^2 −2}^2 =2+(√(2cos 8x)) let cos 8x=2cos^2 8θ ⇒ (q^2 −2)^2 =2+2cos 4θ ⇒ q^2 =2+2cos 2θ q=2cos θ = 2cos [(1/8)cos^(−1) (√((cos 8x)/2))]](Q212278.png)
$$\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}{cos}\mathrm{8}{x}}}}}={q} \\ $$$$\left\{\left({q}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\right\}^{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{2cos}\:\mathrm{8}{x}} \\ $$$${let}\:\:\mathrm{cos}\:\mathrm{8}{x}=\mathrm{2cos}\:^{\mathrm{2}} \mathrm{8}\theta \\ $$$$\Rightarrow\:\:\left({q}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} =\mathrm{2}+\mathrm{2cos}\:\mathrm{4}\theta \\ $$$$\Rightarrow\:{q}^{\mathrm{2}} =\mathrm{2}+\mathrm{2cos}\:\mathrm{2}\theta \\ $$$$\:\:\:\:{q}=\mathrm{2cos}\:\theta\: \\ $$$$\:\:\:\:\:\:=\:\mathrm{2cos}\:\left[\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}^{−\mathrm{1}} \sqrt{\frac{\mathrm{cos}\:\mathrm{8}{x}}{\mathrm{2}}}\right] \\ $$
Commented by TonyCWX08 last updated on 08/Oct/24
$${Nah}\:{its}\:{wrong}. \\ $$$${You}\:{compared}\: \\ $$$${cos}\left(\mathrm{8}{x}\right)\:{and}\:\mathrm{2}{cos}^{\mathrm{2}} \left(\mathrm{8}\theta\right),\:{which}\:{is}\:{two}\:{different}\:{thingd}. \\ $$
Commented by ajfour last updated on 08/Oct/24
$${lets}\:{wait}\:{for}\:{other}\:{expert}\:{comments} \\ $$
Commented by Ghisom last updated on 09/Oct/24

$$\mathrm{it}'\mathrm{s}\:\mathrm{true},\:\mathrm{congratulations}! \\ $$
Commented by Frix last updated on 09/Oct/24

$$\mathrm{Before}\:\mathrm{claiming}\:\mathrm{this}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{or}\:\mathrm{right}\:\mathrm{you} \\ $$$$\mathrm{should}\:\mathrm{check}\:\mathrm{it}.\:\mathrm{Plot}\:\mathrm{it}\:\mathrm{or}\:\mathrm{simply}\:\mathrm{plug}\:\mathrm{in} \\ $$$$\mathrm{some}\:\mathrm{values} \\ $$$$\Rightarrow \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{true}. \\ $$
