Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 138716 by floor(10²Eta[1]) last updated on 17/Apr/21

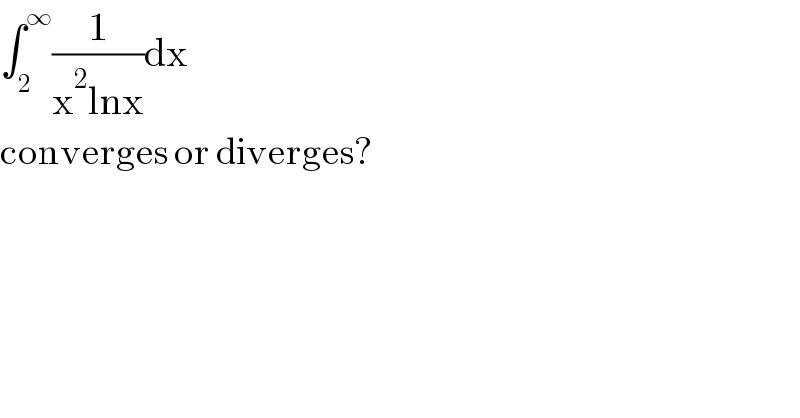
$${\int }_2^{\mathrm{\infty }}\frac{1}{{\mathrm{x}}^2\mathrm{lnx}}\mathrm{dx}$$$$\mathrm{converges}\mathrm{or}\mathrm{diverges}?$$

Answered by mathmax by abdo last updated on 17/Apr/21

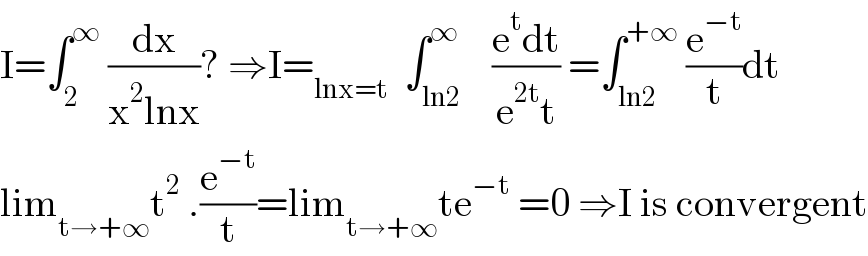
$$\mathrm{I}={\int }_2^{\mathrm{\infty }}\frac{\mathrm{dx}}{{\mathrm{x}}^2\mathrm{lnx}}?\Rightarrow \mathrm{I}{=}_{\mathrm{lnx}=\mathrm{t}}{\int }_{\ln 2}^{\mathrm{\infty }}\frac{{\mathrm{e}}^{\mathrm{t}}\mathrm{dt}}{{\mathrm{e}}^{2\mathrm{t}}\mathrm{t}}={\int }_{\ln 2}^{+\mathrm{\infty }}\frac{{\mathrm{e}}^{-\mathrm{t}}}{\mathrm{t}}\mathrm{dt}$$$${\lim }_{\mathrm{t}\to +\mathrm{\infty }}{\mathrm{t}}^2.\frac{{\mathrm{e}}^{-\mathrm{t}}}{\mathrm{t}}={\lim }_{\mathrm{t}\to +\mathrm{\infty }}{\mathrm{te}}^{-\mathrm{t}}=0\Rightarrow \mathrm{I}\mathrm{is}\mathrm{convergent}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com