Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 199900 by Calculusboy last updated on 11/Nov/23

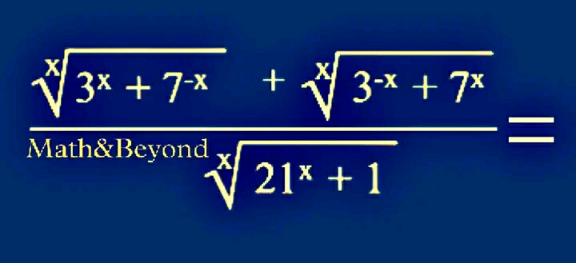
Answered by Rasheed.Sindhi last updated on 11/Nov/23

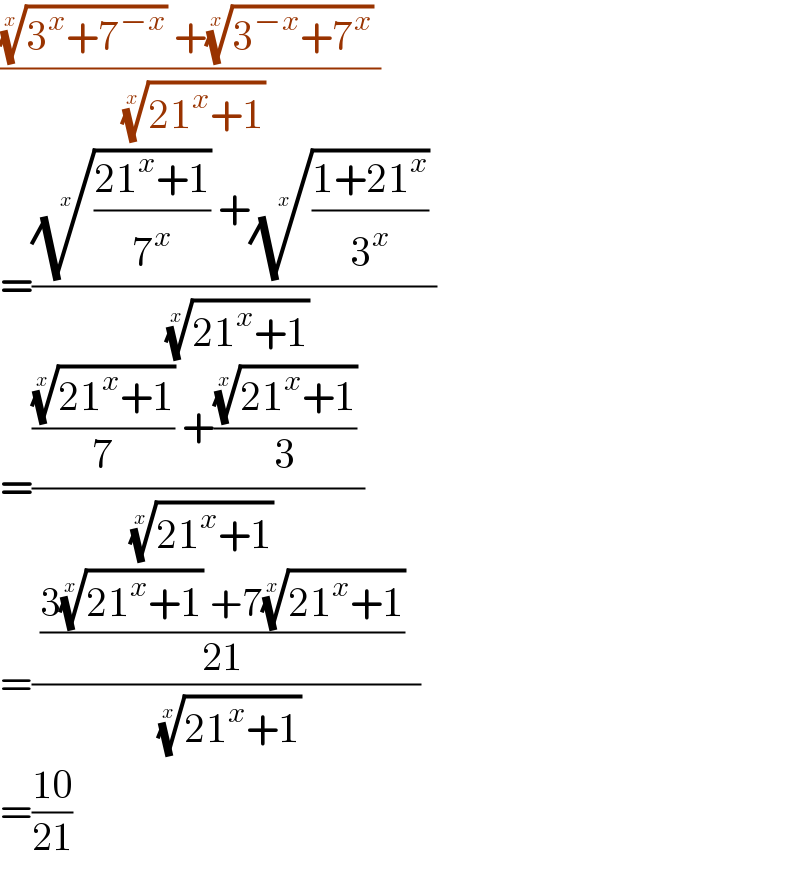
((((3^x +7^(−x) ))^(1/x) +((3^(−x) +7^x ))^(1/x) )/( ((21^x +1))^(1/x) )) =(((((21^x +1)/7^x ))^(1/x) +(((1+21^x )/3^x ))^(1/x) )/( ((21^x +1))^(1/x) )) =(((((21^x +1))^(1/x) /7) +(((21^x +1))^(1/x) /3) )/( ((21^x +1))^(1/x) )) =(( ((3((21^x +1))^(1/x) +7((21^x +1))^(1/x) )/(21)) )/( ((21^x +1))^(1/x) )) =((10)/(21))

$$\frac{\sqrt[{{x}}]{\mathrm{3}^{{x}} +\mathrm{7}^{−{x}} }\:+\sqrt[{{x}}]{\mathrm{3}^{−{x}} +\mathrm{7}^{{x}} }\:}{\:\sqrt[{{x}}]{\mathrm{21}^{{x}} +\mathrm{1}}} \\ $$$$=\frac{\sqrt[{{x}}]{\frac{\mathrm{21}^{{x}} +\mathrm{1}}{\mathrm{7}^{{x}} }}\:+\sqrt[{{x}}]{\frac{\mathrm{1}+\mathrm{21}^{{x}} }{\mathrm{3}^{{x}} }}\:}{\:\sqrt[{{x}}]{\mathrm{21}^{{x}} +\mathrm{1}}} \\ $$$$=\frac{\frac{\sqrt[{{x}}]{\mathrm{21}^{{x}} +\mathrm{1}}}{\mathrm{7}}\:+\frac{\sqrt[{{x}}]{\mathrm{21}^{{x}} +\mathrm{1}}}{\mathrm{3}}\:}{\:\sqrt[{{x}}]{\mathrm{21}^{{x}} +\mathrm{1}}} \\ $$$$=\frac{\:\frac{\mathrm{3}\sqrt[{{x}}]{\mathrm{21}^{{x}} +\mathrm{1}}\:+\mathrm{7}\sqrt[{{x}}]{\mathrm{21}^{{x}} +\mathrm{1}}}{\mathrm{21}}\:\:}{\:\sqrt[{{x}}]{\mathrm{21}^{{x}} +\mathrm{1}}} \\ $$$$=\frac{\mathrm{10}}{\mathrm{21}} \\ $$

Answered by Rasheed.Sindhi last updated on 11/Nov/23

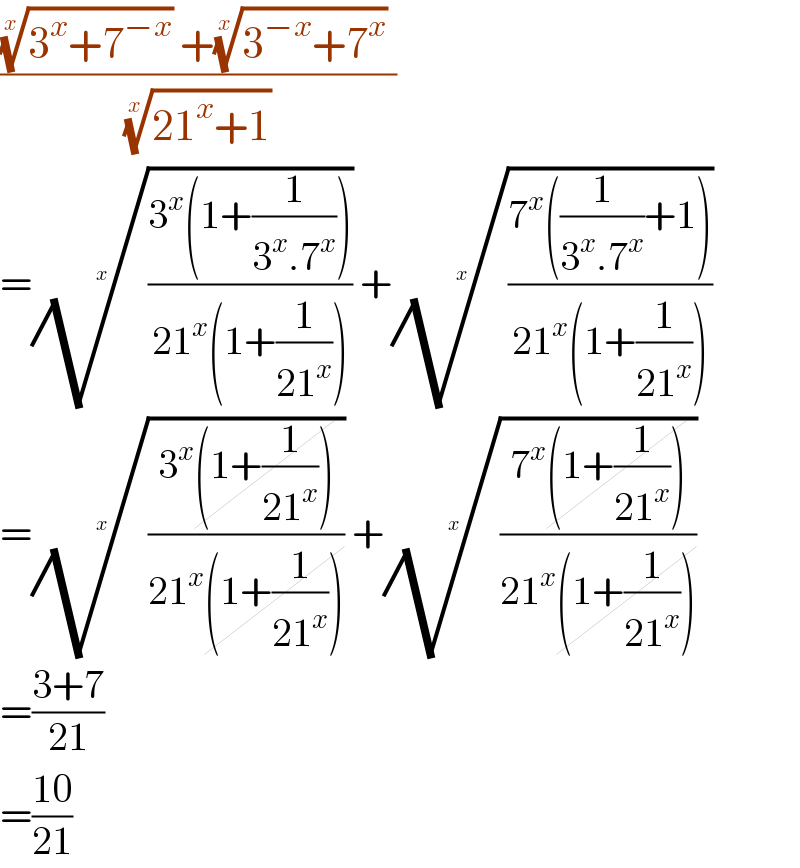
((((3^x +7^(−x) ))^(1/x) +((3^(−x) +7^x ))^(1/x) )/( ((21^x +1))^(1/x) )) =(((3^x (1+(1/(3^x .7^x ))))/(21^x (1+(1/(21^x ))))))^(1/x) +(((7^x ((1/(3^x .7^x ))+1))/(21^x (1+(1/(21^x ))))))^(1/x) =(((3^x (1+(1/(21^x ))))/(21^x (1+(1/(21^x ))))))^(1/x) +(((7^x (1+(1/(21^x ))))/(21^x (1+(1/(21^x ))))))^(1/x) =((3+7)/(21)) =((10)/(21))

$$\frac{\sqrt[{{x}}]{\mathrm{3}^{{x}} +\mathrm{7}^{−{x}} }\:+\sqrt[{{x}}]{\mathrm{3}^{−{x}} +\mathrm{7}^{{x}} }\:}{\:\sqrt[{{x}}]{\mathrm{21}^{{x}} +\mathrm{1}}\:} \\ $$$$=\sqrt[{{x}}]{\frac{\mathrm{3}^{{x}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{{x}} .\mathrm{7}^{{x}} }\right)}{\mathrm{21}^{{x}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{21}^{{x}} }\right)}}\:+\sqrt[{{x}}]{\frac{\mathrm{7}^{{x}} \left(\frac{\mathrm{1}}{\mathrm{3}^{{x}} .\mathrm{7}^{{x}} }+\mathrm{1}\right)}{\mathrm{21}^{{x}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{21}^{{x}} }\right)}} \\ $$$$=\sqrt[{{x}}]{\frac{\mathrm{3}^{{x}} \cancel{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{21}^{{x}} }\right)}}{\mathrm{21}^{{x}} \cancel{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{21}^{{x}} }\right)}}}\:+\sqrt[{{x}}]{\frac{\mathrm{7}^{{x}} \cancel{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{21}^{{x}} }\right)}}{\mathrm{21}^{{x}} \cancel{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{21}^{{x}} }\right)}}} \\ $$$$=\frac{\mathrm{3}+\mathrm{7}}{\mathrm{21}} \\ $$$$=\frac{\mathrm{10}}{\mathrm{21}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com