
Question Number 199899 by sonukgindia last updated on 11/Nov/23

Answered by Rajpurohith last updated on 11/Nov/23
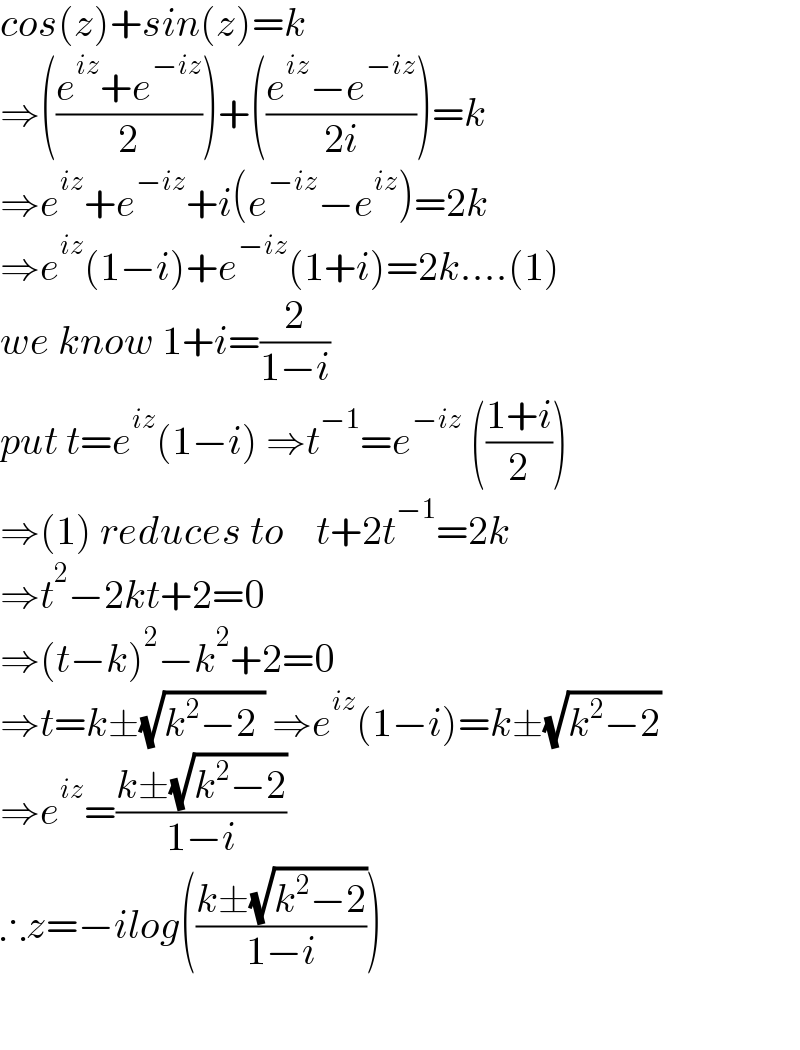
$${cos}\left({z}\right)+{sin}\left({z}\right)={k}\: \\ $$$$\Rightarrow\left(\frac{{e}^{{iz}} +{e}^{−{iz}} }{\mathrm{2}}\right)+\left(\frac{{e}^{{iz}} −{e}^{−{iz}} }{\mathrm{2}{i}}\right)={k} \\ $$$$\Rightarrow{e}^{{iz}} +{e}^{−{iz}} +{i}\left({e}^{−{iz}} −{e}^{{iz}} \right)=\mathrm{2}{k} \\ $$$$\Rightarrow{e}^{{iz}} \left(\mathrm{1}−{i}\right)+{e}^{−{iz}} \left(\mathrm{1}+{i}\right)=\mathrm{2}{k}....\left(\mathrm{1}\right) \\ $$$${we}\:{know}\:\mathrm{1}+{i}=\frac{\mathrm{2}}{\mathrm{1}−{i}} \\ $$$${put}\:{t}={e}^{{iz}} \left(\mathrm{1}−{i}\right)\:\Rightarrow{t}^{−\mathrm{1}} ={e}^{−{iz}} \:\left(\frac{\mathrm{1}+{i}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\left(\mathrm{1}\right)\:{reduces}\:{to}\:\:\:\:{t}+\mathrm{2}{t}^{−\mathrm{1}} =\mathrm{2}{k} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{2}{kt}+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\left({t}−{k}\right)^{\mathrm{2}} −{k}^{\mathrm{2}} +\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow{t}={k}\pm\sqrt{{k}^{\mathrm{2}} −\mathrm{2}\:}\:\Rightarrow{e}^{{iz}} \left(\mathrm{1}−{i}\right)={k}\pm\sqrt{{k}^{\mathrm{2}} −\mathrm{2}} \\ $$$$\Rightarrow{e}^{{iz}} =\frac{{k}\pm\sqrt{{k}^{\mathrm{2}} −\mathrm{2}}}{\mathrm{1}−{i}} \\ $$$$\therefore{z}=−{ilog}\left(\frac{{k}\pm\sqrt{{k}^{\mathrm{2}} −\mathrm{2}}}{\mathrm{1}−{i}}\right) \\ $$$$ \\ $$
