
Question Number 199840 by Calculusboy last updated on 10/Nov/23
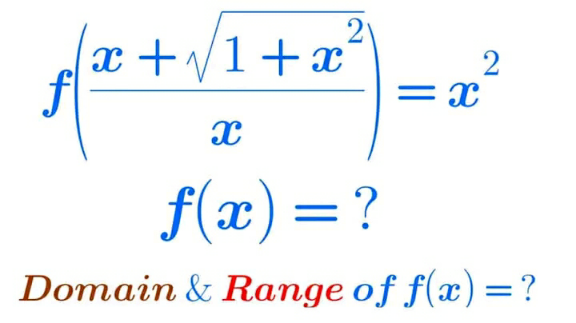
Answered by deleteduser1 last updated on 10/Nov/23
![Let ((y+(√(1+y^2 )))/y)=1+(√((1/y^2 )+1))=x ⇒x^2 −2x=(1/y^2 )⇒y=(√(1/(x^2 −2x))) ⇒f(x)=(1/(x^2 −2x))⇒x∈R\(0,2) [f(x)=(1/(x^2 −2x))>0⇒x^2 −2x>0⇒(x−1)^2 >1⇒R\(0,2)]](Q199852.png)
$${Let}\:\frac{{y}+\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }}{{y}}=\mathrm{1}+\sqrt{\frac{\mathrm{1}}{{y}^{\mathrm{2}} }+\mathrm{1}}={x} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{x}=\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\Rightarrow{y}=\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{2}{x}}} \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{2}{x}}\Rightarrow{x}\in\mathbb{R}\backslash\left(\mathrm{0},\mathrm{2}\right) \\ $$$$\left[{f}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{2}{x}}>\mathrm{0}\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{x}>\mathrm{0}\Rightarrow\left({x}−\mathrm{1}\right)^{\mathrm{2}} >\mathrm{1}\Rightarrow{R}\backslash\left(\mathrm{0},\mathrm{2}\right)\right] \\ $$
Commented by Calculusboy last updated on 10/Nov/23

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$
