
Question Number 199830 by cortano12 last updated on 10/Nov/23
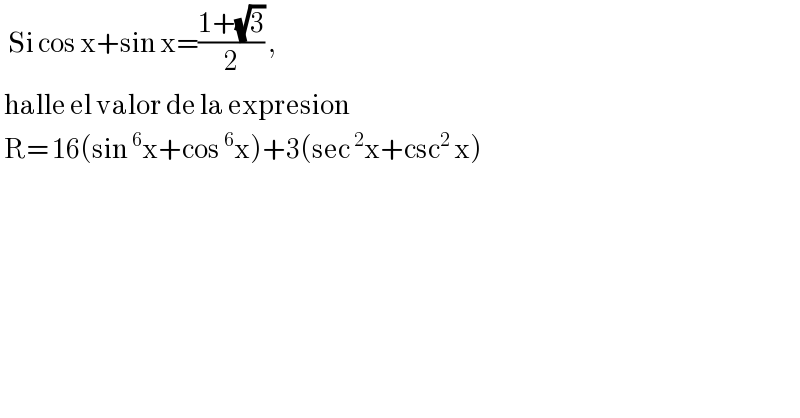
$$\:\:\mathrm{Si}\:\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}=\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:, \\ $$$$\:\mathrm{halle}\:\mathrm{el}\:\mathrm{valor}\:\mathrm{de}\:\mathrm{la}\:\mathrm{expresion}\: \\ $$$$\:\mathrm{R}=\:\mathrm{16}\left(\mathrm{sin}\:^{\mathrm{6}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{6}} \mathrm{x}\right)+\mathrm{3}\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}+\mathrm{csc}^{\mathrm{2}} \:\mathrm{x}\right) \\ $$
Answered by Frix last updated on 10/Nov/23
![cos x +sin x =c ⇒ x=2tan^(−1) ((1±(√(2−c^2 )))/(c+1)) [+2nπ] c=((1+(√3))/2) ⇒ x=(π/6)∨x=(π/3) R=23](Q199880.png)
$$\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}\:={c}\:\Rightarrow \\ $$$${x}=\mathrm{2tan}^{−\mathrm{1}} \:\frac{\mathrm{1}\pm\sqrt{\mathrm{2}−{c}^{\mathrm{2}} }}{{c}+\mathrm{1}}\:\left[+\mathrm{2}{n}\pi\right] \\ $$$${c}=\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow\:{x}=\frac{\pi}{\mathrm{6}}\vee{x}=\frac{\pi}{\mathrm{3}} \\ $$$${R}=\mathrm{23} \\ $$
