
Question Number 199825 by cortano12 last updated on 10/Nov/23

Answered by mr W last updated on 10/Nov/23
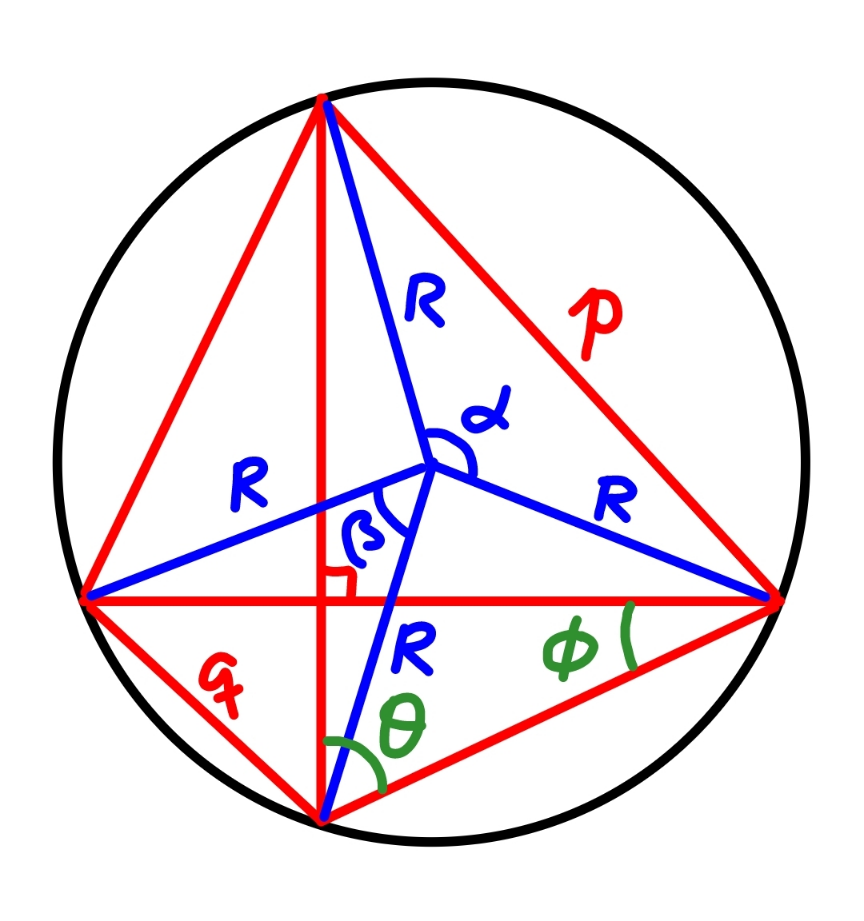
Commented by mr W last updated on 10/Nov/23
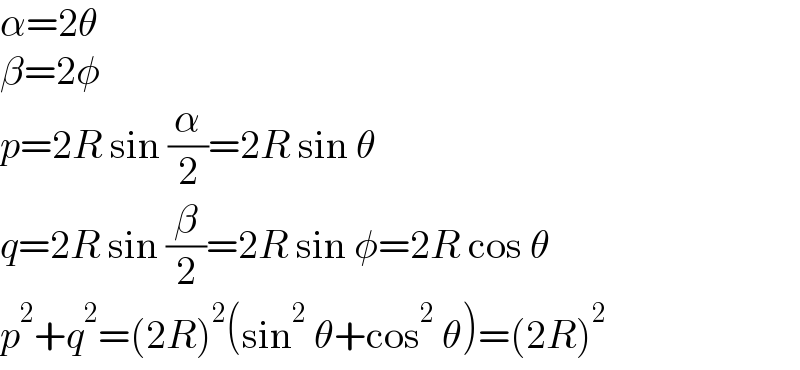
$$\alpha=\mathrm{2}\theta \\ $$$$\beta=\mathrm{2}\phi \\ $$$${p}=\mathrm{2}{R}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}=\mathrm{2}{R}\:\mathrm{sin}\:\theta \\ $$$${q}=\mathrm{2}{R}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}=\mathrm{2}{R}\:\mathrm{sin}\:\phi=\mathrm{2}{R}\:\mathrm{cos}\:\theta \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\left(\mathrm{2}{R}\right)^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta\right)=\left(\mathrm{2}{R}\right)^{\mathrm{2}} \\ $$
