
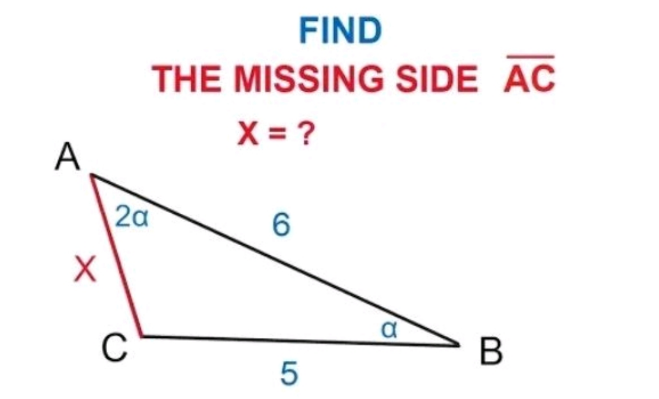
Question Number 199770 by Rupesh123 last updated on 09/Nov/23
Answered by aleks041103 last updated on 09/Nov/23
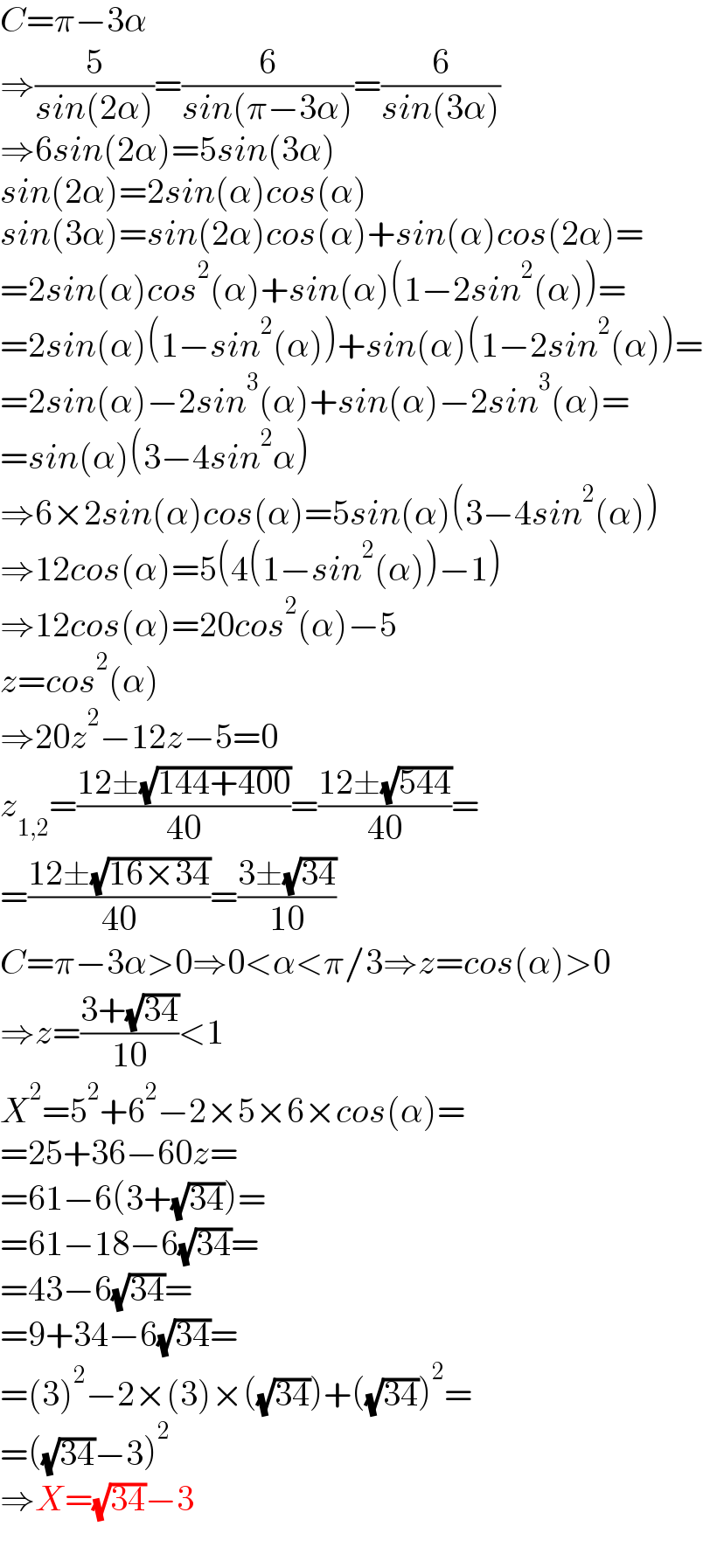
$${C}=\pi−\mathrm{3}\alpha \\ $$$$\Rightarrow\frac{\mathrm{5}}{{sin}\left(\mathrm{2}\alpha\right)}=\frac{\mathrm{6}}{{sin}\left(\pi−\mathrm{3}\alpha\right)}=\frac{\mathrm{6}}{{sin}\left(\mathrm{3}\alpha\right)} \\ $$$$\Rightarrow\mathrm{6}{sin}\left(\mathrm{2}\alpha\right)=\mathrm{5}{sin}\left(\mathrm{3}\alpha\right) \\ $$$${sin}\left(\mathrm{2}\alpha\right)=\mathrm{2}{sin}\left(\alpha\right){cos}\left(\alpha\right) \\ $$$${sin}\left(\mathrm{3}\alpha\right)={sin}\left(\mathrm{2}\alpha\right){cos}\left(\alpha\right)+{sin}\left(\alpha\right){cos}\left(\mathrm{2}\alpha\right)= \\ $$$$=\mathrm{2}{sin}\left(\alpha\right){cos}^{\mathrm{2}} \left(\alpha\right)+{sin}\left(\alpha\right)\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \left(\alpha\right)\right)= \\ $$$$=\mathrm{2}{sin}\left(\alpha\right)\left(\mathrm{1}−{sin}^{\mathrm{2}} \left(\alpha\right)\right)+{sin}\left(\alpha\right)\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \left(\alpha\right)\right)= \\ $$$$=\mathrm{2}{sin}\left(\alpha\right)−\mathrm{2}{sin}^{\mathrm{3}} \left(\alpha\right)+{sin}\left(\alpha\right)−\mathrm{2}{sin}^{\mathrm{3}} \left(\alpha\right)= \\ $$$$={sin}\left(\alpha\right)\left(\mathrm{3}−\mathrm{4}{sin}^{\mathrm{2}} \alpha\right) \\ $$$$\Rightarrow\mathrm{6}×\mathrm{2}{sin}\left(\alpha\right){cos}\left(\alpha\right)=\mathrm{5}{sin}\left(\alpha\right)\left(\mathrm{3}−\mathrm{4}{sin}^{\mathrm{2}} \left(\alpha\right)\right) \\ $$$$\Rightarrow\mathrm{12}{cos}\left(\alpha\right)=\mathrm{5}\left(\mathrm{4}\left(\mathrm{1}−{sin}^{\mathrm{2}} \left(\alpha\right)\right)−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{12}{cos}\left(\alpha\right)=\mathrm{20}{cos}^{\mathrm{2}} \left(\alpha\right)−\mathrm{5} \\ $$$${z}={cos}^{\mathrm{2}} \left(\alpha\right) \\ $$$$\Rightarrow\mathrm{20}{z}^{\mathrm{2}} −\mathrm{12}{z}−\mathrm{5}=\mathrm{0} \\ $$$${z}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{12}\pm\sqrt{\mathrm{144}+\mathrm{400}}}{\mathrm{40}}=\frac{\mathrm{12}\pm\sqrt{\mathrm{544}}}{\mathrm{40}}= \\ $$$$=\frac{\mathrm{12}\pm\sqrt{\mathrm{16}×\mathrm{34}}}{\mathrm{40}}=\frac{\mathrm{3}\pm\sqrt{\mathrm{34}}}{\mathrm{10}} \\ $$$${C}=\pi−\mathrm{3}\alpha>\mathrm{0}\Rightarrow\mathrm{0}<\alpha<\pi/\mathrm{3}\Rightarrow{z}={cos}\left(\alpha\right)>\mathrm{0} \\ $$$$\Rightarrow{z}=\frac{\mathrm{3}+\sqrt{\mathrm{34}}}{\mathrm{10}}<\mathrm{1} \\ $$$${X}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} −\mathrm{2}×\mathrm{5}×\mathrm{6}×{cos}\left(\alpha\right)= \\ $$$$=\mathrm{25}+\mathrm{36}−\mathrm{60}{z}= \\ $$$$=\mathrm{61}−\mathrm{6}\left(\mathrm{3}+\sqrt{\mathrm{34}}\right)= \\ $$$$=\mathrm{61}−\mathrm{18}−\mathrm{6}\sqrt{\mathrm{34}}= \\ $$$$=\mathrm{43}−\mathrm{6}\sqrt{\mathrm{34}}= \\ $$$$=\mathrm{9}+\mathrm{34}−\mathrm{6}\sqrt{\mathrm{34}}= \\ $$$$=\left(\mathrm{3}\right)^{\mathrm{2}} −\mathrm{2}×\left(\mathrm{3}\right)×\left(\sqrt{\mathrm{34}}\right)+\left(\sqrt{\mathrm{34}}\right)^{\mathrm{2}} = \\ $$$$=\left(\sqrt{\mathrm{34}}−\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{X}=\sqrt{\mathrm{34}}−\mathrm{3} \\ $$
Commented by Mingma last updated on 09/Nov/23
Nice, solution
Answered by mr W last updated on 09/Nov/23
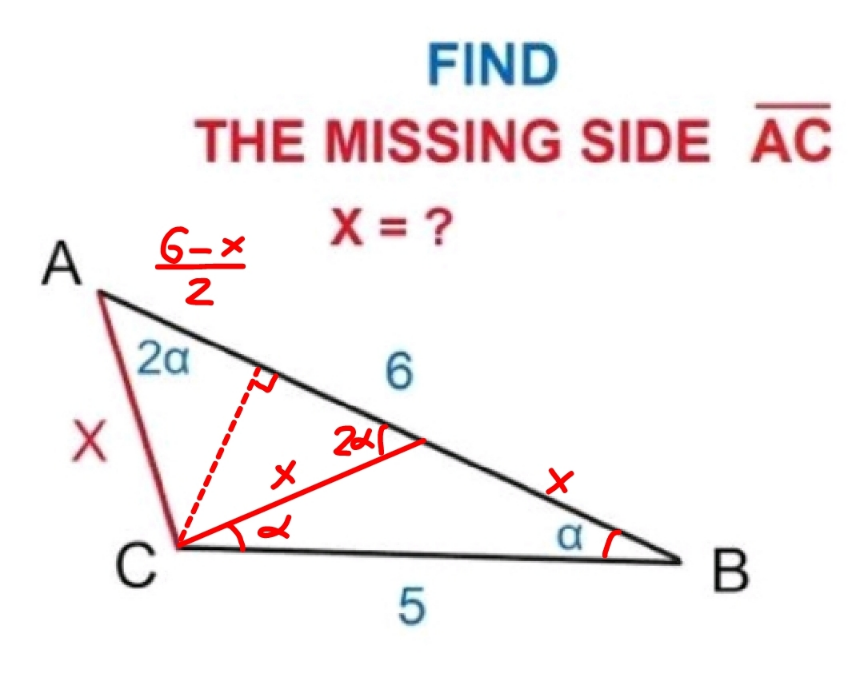
Commented by mr W last updated on 09/Nov/23
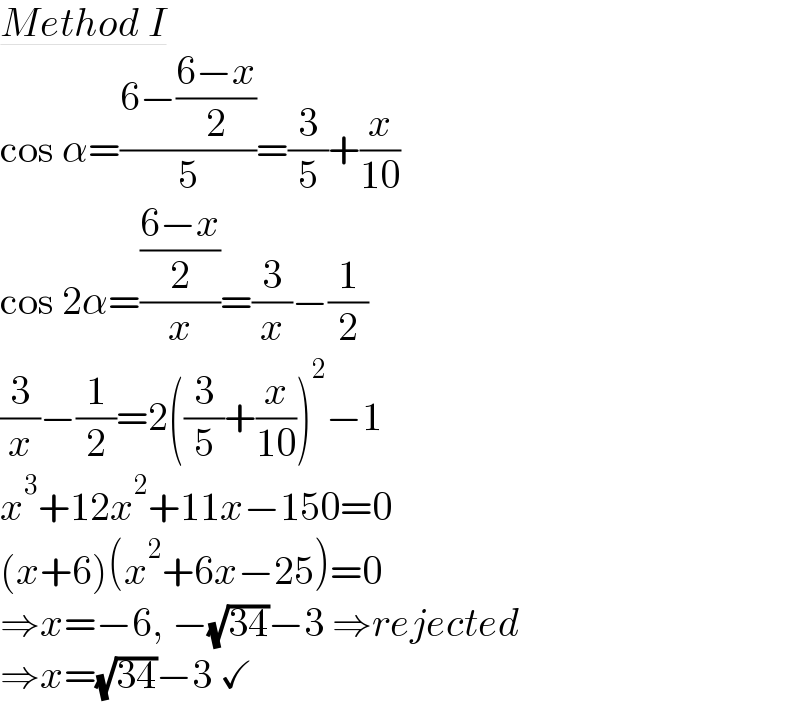
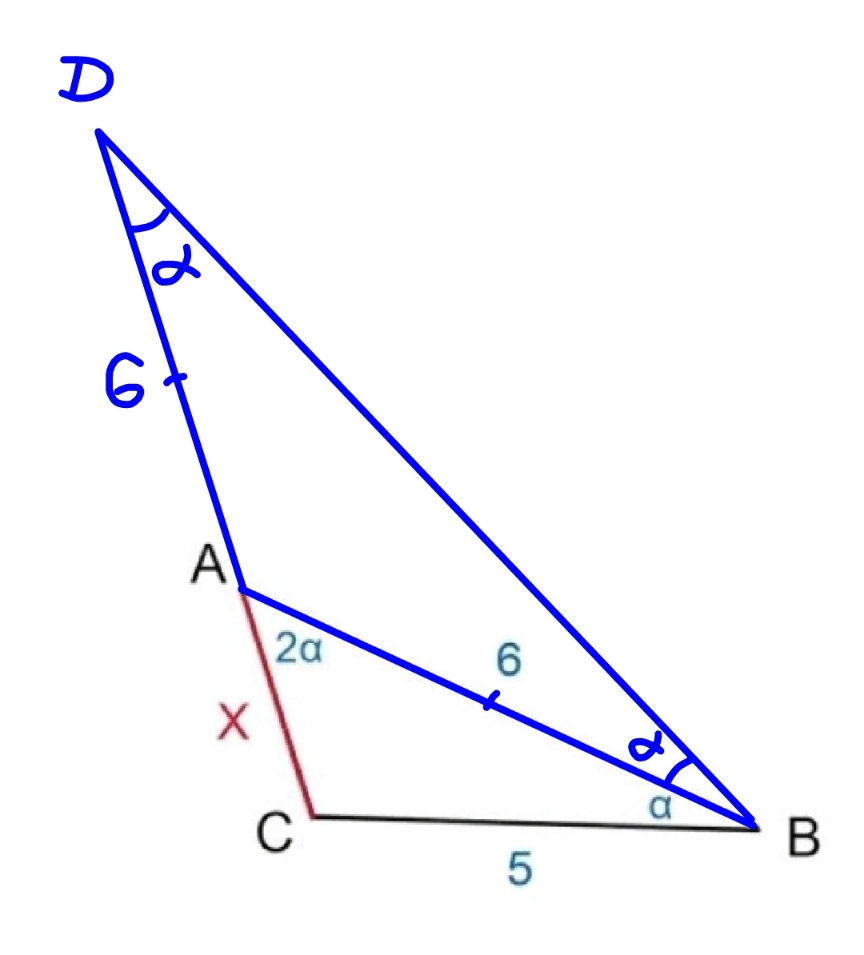
$$\underline{{Method}\:{I}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{6}−\frac{\mathrm{6}−{x}}{\mathrm{2}}}{\mathrm{5}}=\frac{\mathrm{3}}{\mathrm{5}}+\frac{{x}}{\mathrm{10}} \\ $$$$\mathrm{cos}\:\mathrm{2}\alpha=\frac{\frac{\mathrm{6}−{x}}{\mathrm{2}}}{{x}}=\frac{\mathrm{3}}{{x}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{3}}{{x}}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{5}}+\frac{{x}}{\mathrm{10}}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$${x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{11}{x}−\mathrm{150}=\mathrm{0} \\ $$$$\left({x}+\mathrm{6}\right)\left({x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{25}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{6},\:−\sqrt{\mathrm{34}}−\mathrm{3}\:\Rightarrow{rejected} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{34}}−\mathrm{3}\:\checkmark \\ $$
Commented by aleks041103 last updated on 09/Nov/23
$${Veru}\:{nice}\:{and}\:{elegant}!\:{Bravo}!! \\ $$
Commented by mr W last updated on 09/Nov/23

$${thanks}\:{sir}! \\ $$
Commented by Mingma last updated on 09/Nov/23
Nice solution!
Answered by mr W last updated on 09/Nov/23
Commented by mr W last updated on 09/Nov/23
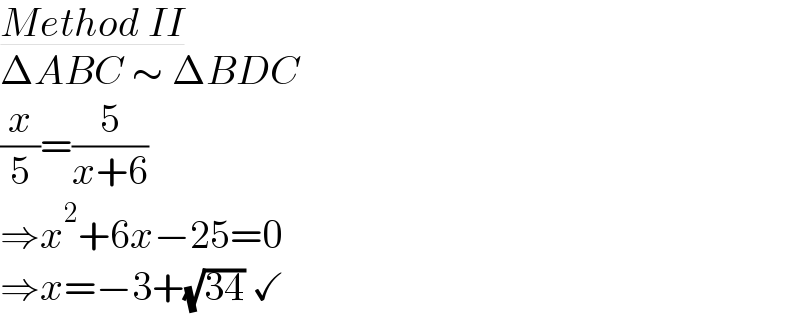
$$\underline{{Method}\:{II}} \\ $$$$\Delta{ABC}\:\sim\:\Delta{BDC} \\ $$$$\frac{{x}}{\mathrm{5}}=\frac{\mathrm{5}}{{x}+\mathrm{6}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{25}=\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{3}+\sqrt{\mathrm{34}}\:\checkmark \\ $$
Commented by Mingma last updated on 09/Nov/23
Nice solution!
Answered by ajfour last updated on 09/Nov/23
Commented by ajfour last updated on 09/Nov/23
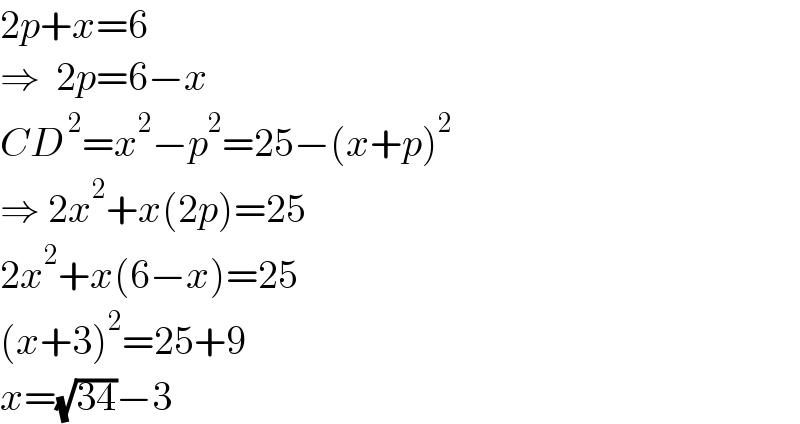
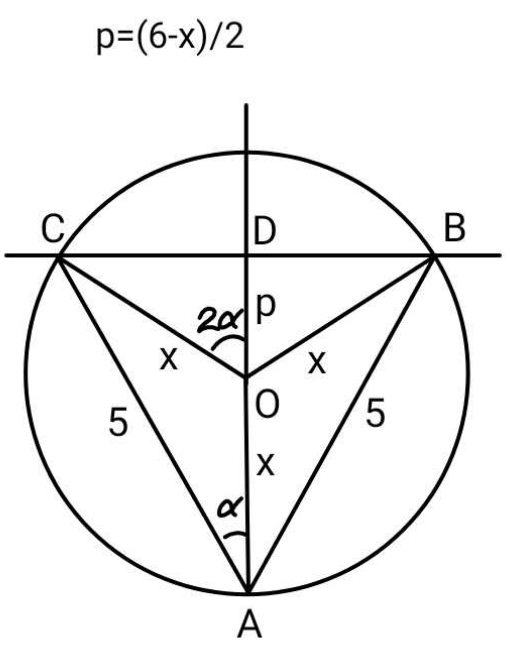
$$\mathrm{2}{p}+{x}=\mathrm{6} \\ $$$$\Rightarrow\:\:\mathrm{2}{p}=\mathrm{6}−{x} \\ $$$${CD}^{\:\mathrm{2}} ={x}^{\mathrm{2}} −{p}^{\mathrm{2}} =\mathrm{25}−\left({x}+{p}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{2}{x}^{\mathrm{2}} +{x}\left(\mathrm{2}{p}\right)=\mathrm{25} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +{x}\left(\mathrm{6}−{x}\right)=\mathrm{25} \\ $$$$\left({x}+\mathrm{3}\right)^{\mathrm{2}} =\mathrm{25}+\mathrm{9} \\ $$$${x}=\sqrt{\mathrm{34}}−\mathrm{3} \\ $$
