
Question Number 199728 by Mingma last updated on 08/Nov/23
Answered by deleteduser1 last updated on 08/Nov/23
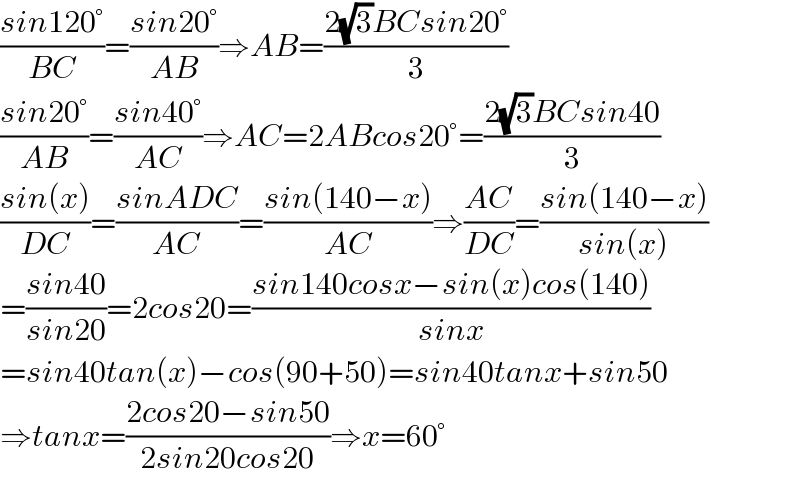
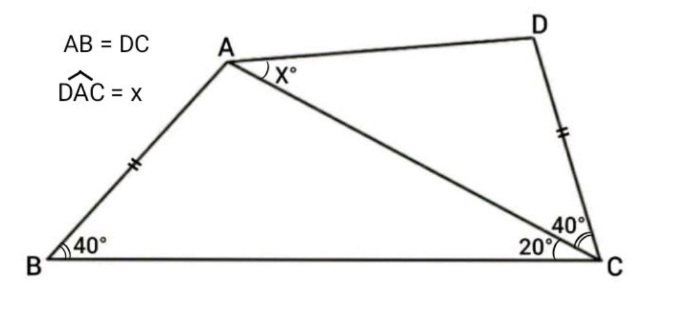
$$\frac{{sin}\mathrm{120}°}{{BC}}=\frac{{sin}\mathrm{20}°}{{AB}}\Rightarrow{AB}=\frac{\mathrm{2}\sqrt{\mathrm{3}}{BCsin}\mathrm{20}°}{\mathrm{3}} \\ $$$$\frac{{sin}\mathrm{20}°}{{AB}}=\frac{{sin}\mathrm{40}°}{{AC}}\Rightarrow{AC}=\mathrm{2}{ABcos}\mathrm{20}°=\frac{\mathrm{2}\sqrt{\mathrm{3}}{BCsin}\mathrm{40}}{\mathrm{3}} \\ $$$$\frac{{sin}\left({x}\right)}{{DC}}=\frac{{sinADC}}{{AC}}=\frac{{sin}\left(\mathrm{140}−{x}\right)}{{AC}}\Rightarrow\frac{{AC}}{{DC}}=\frac{{sin}\left(\mathrm{140}−{x}\right)}{{sin}\left({x}\right)} \\ $$$$=\frac{{sin}\mathrm{40}}{{sin}\mathrm{20}}=\mathrm{2}{cos}\mathrm{20}=\frac{{sin}\mathrm{140}{cosx}−{sin}\left({x}\right){cos}\left(\mathrm{140}\right)}{{sinx}} \\ $$$$={sin}\mathrm{40}{tan}\left({x}\right)−{cos}\left(\mathrm{90}+\mathrm{50}\right)={sin}\mathrm{40}{tanx}+{sin}\mathrm{50} \\ $$$$\Rightarrow{tanx}=\frac{\mathrm{2}{cos}\mathrm{20}−{sin}\mathrm{50}}{\mathrm{2}{sin}\mathrm{20}{cos}\mathrm{20}}\Rightarrow{x}=\mathrm{60}° \\ $$
Commented by Rupesh123 last updated on 08/Nov/23
Perfect, sir!
