
Question Number 199620 by Mingma last updated on 06/Nov/23
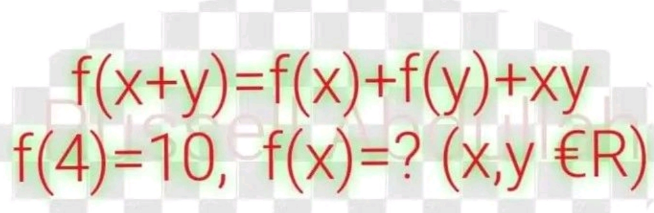
Answered by witcher3 last updated on 06/Nov/23

$$\mathrm{f}\left(\mathrm{4}\right)=\mathrm{f}\left(\mathrm{2}+\mathrm{2}\right)=\mathrm{2f}\left(\mathrm{2}\right)+\mathrm{4}=\mathrm{10}\Rightarrow\mathrm{f}\left(\mathrm{2}\right)=\mathrm{3} \\ $$$$\mathrm{f}\left(\mathrm{2}\right)=\mathrm{2f}\left(\mathrm{1}\right)+\mathrm{1}=\mathrm{3}\Rightarrow\mathrm{f}\left(\mathrm{1}\right)=\mathrm{1},\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}+\mathrm{x} \\ $$$$\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\left(\mathrm{f}\left(\mathrm{k}+\mathrm{1}\right)−\mathrm{f}\left(\mathrm{k}\right)\right)=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{2}}\:\:\mathrm{solution}\:\mathrm{if}\:\mathrm{f}\:\mathrm{is}\:\mathrm{continus}\:\mathrm{we}\:\mathrm{can}\:\mathrm{show}\:\mathrm{that}\:\mathrm{is} \\ $$$$\mathrm{unique} \\ $$$$\mathrm{f}\in\mathrm{C}_{\mathrm{0}} \mathrm{solution}\:\mathrm{suppose}\:\exists\mathrm{g}\in\mathrm{C}_{\mathrm{0}} \:\mathrm{also}\:\mathrm{solution} \\ $$$$\mathrm{g}\left(\mathrm{4}\right)=\mathrm{f}\left(\mathrm{4}\right)=\mathrm{10} \\ $$$$\:\mathrm{h}=\mathrm{g}−\mathrm{f}\:\Rightarrow\mathrm{h}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{h}\left(\mathrm{x}\right)+\mathrm{h}\left(\mathrm{y}\right) \\ $$$$\mathrm{h}\left(\mathrm{0}\right)=\mathrm{h}\left(\mathrm{1}\right)=\mathrm{h}\left(\mathrm{2}\right)=\mathrm{h}\left(\mathrm{4}\right)=\mathrm{0},\forall\mathrm{n}\in\mathbb{N}\:\mathrm{h}\left(\mathrm{n}\right)=\mathrm{0}\:\mathrm{because} \\ $$$$``\mathrm{f}\left(\mathrm{n}\right)=\mathrm{g}\left(\mathrm{n}\right)\:'' \\ $$$$\mathrm{h}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{h}\left(\mathrm{x}\right)+\mathrm{h}\left(\mathrm{y}\right) \\ $$$$\Rightarrow\mathrm{h}\left(\mathrm{n}\right)=\mathrm{nh}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{h}\left(\frac{\mathrm{p}}{\mathrm{q}}\right)=\frac{\mathrm{p}}{\mathrm{q}}\mathrm{h}\left(\mathrm{1}\right)=\mathrm{0}\Rightarrow\forall\mathrm{x}\in\mathrm{IQ}\:\mathrm{h}\left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\mathrm{by}\:\mathrm{densite}\:\mathrm{Q}\:\mathrm{over}\:\mathrm{IR}\:\mathrm{and}\:\mathrm{contiuity}\:\mathrm{of}\:\mathrm{h} \\ $$$$\forall\mathrm{x}\in\mathbb{R}\:\exists\mathrm{x}_{\mathrm{n}} \in\mathrm{IQ}\:\mathrm{x}_{\mathrm{n}} \rightarrow\mathrm{x} \\ $$$$\mathrm{h}\left(\mathrm{x}_{\mathrm{n}} \right)=\mathrm{0}\Rightarrow\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}h}\left(\mathrm{x}_{\mathrm{n}} \right)=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}0}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{h}\left(\mathrm{x}\right)=\mathrm{0},\forall\mathrm{x}\in\mathbb{R} \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}\right)\:\Rightarrow\:\mathrm{f}\:\mathrm{is}\:\mathrm{unique} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{2}} \\ $$$$ \\ $$
Commented by Mingma last updated on 06/Nov/23
Nice one!
Commented by witcher3 last updated on 06/Nov/23

$$\mathrm{withe}\:\mathrm{Pleasur} \\ $$
