
Question Number 199602 by hardmath last updated on 05/Nov/23
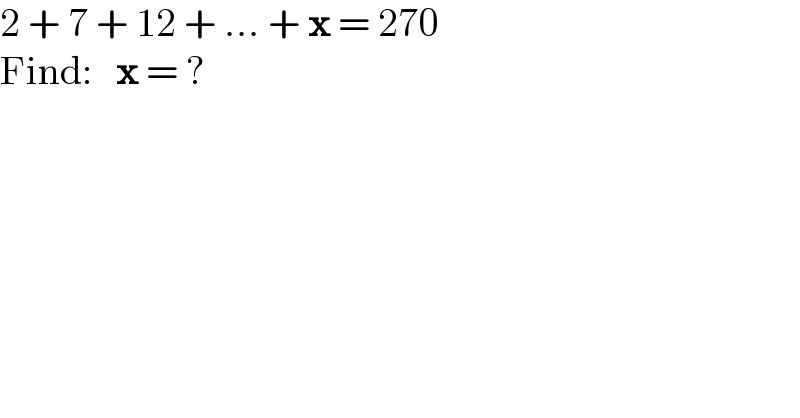
$$\mathrm{2}\:+\:\mathrm{7}\:+\:\mathrm{12}\:+\:...\:+\:\boldsymbol{\mathrm{x}}\:=\:\mathrm{270} \\ $$$$\mathrm{Find}:\:\:\:\boldsymbol{\mathrm{x}}\:=\:? \\ $$
Answered by Rasheed.Sindhi last updated on 06/Nov/23
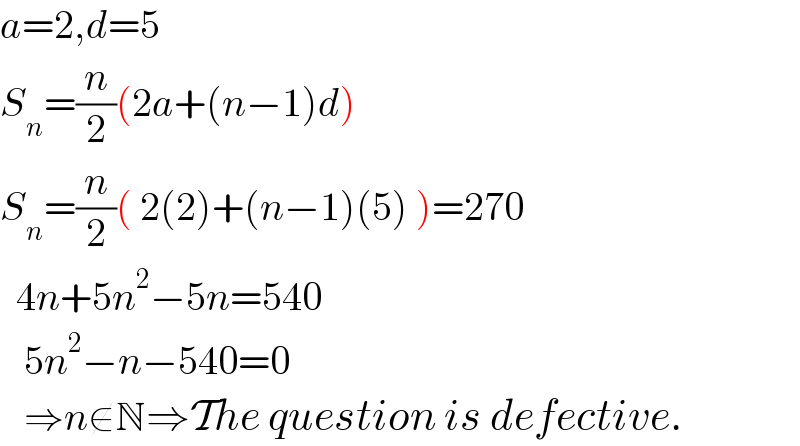
$${a}=\mathrm{2},{d}=\mathrm{5} \\ $$$${S}_{{n}} =\frac{{n}}{\mathrm{2}}\left(\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right) \\ $$$${S}_{{n}} =\frac{{n}}{\mathrm{2}}\left(\:\mathrm{2}\left(\mathrm{2}\right)+\left({n}−\mathrm{1}\right)\left(\mathrm{5}\right)\:\right)=\mathrm{270} \\ $$$$\:\:\mathrm{4}{n}+\mathrm{5}{n}^{\mathrm{2}} −\mathrm{5}{n}=\mathrm{540} \\ $$$$\:\:\:\mathrm{5}{n}^{\mathrm{2}} −{n}−\mathrm{540}=\mathrm{0} \\ $$$$\:\:\:\Rightarrow{n}\notin\mathbb{N}\Rightarrow\mathcal{T}{he}\:{question}\:{is}\:{defective}. \\ $$
Answered by emilagazade last updated on 05/Nov/23
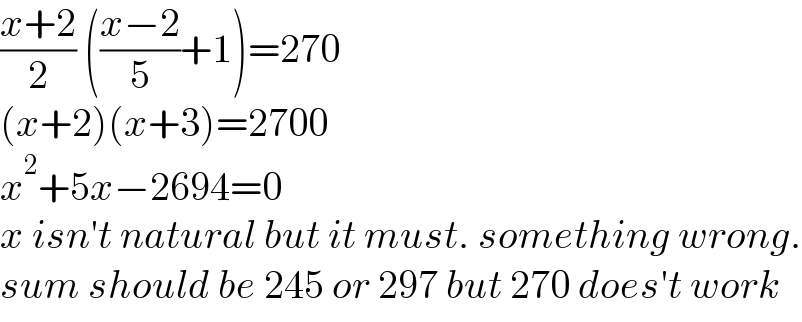
$$\frac{{x}+\mathrm{2}}{\mathrm{2}}\:\left(\frac{{x}−\mathrm{2}}{\mathrm{5}}+\mathrm{1}\right)=\mathrm{270} \\ $$$$\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)=\mathrm{2700} \\ $$$${x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{2694}=\mathrm{0} \\ $$$${x}\:{isn}'{t}\:{natural}\:{but}\:{it}\:{must}.\:{something}\:{wrong}. \\ $$$${sum}\:{should}\:{be}\:\mathrm{245}\:{or}\:\mathrm{297}\:{but}\:\mathrm{270}\:{does}'{t}\:{work} \\ $$
Answered by Frix last updated on 05/Nov/23
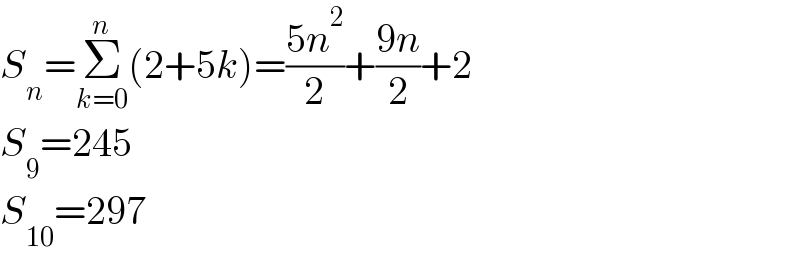
$${S}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{2}+\mathrm{5}{k}\right)=\frac{\mathrm{5}{n}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{9}{n}}{\mathrm{2}}+\mathrm{2} \\ $$$${S}_{\mathrm{9}} =\mathrm{245} \\ $$$${S}_{\mathrm{10}} =\mathrm{297} \\ $$
