Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 199405 by mnjuly1970 last updated on 03/Nov/23

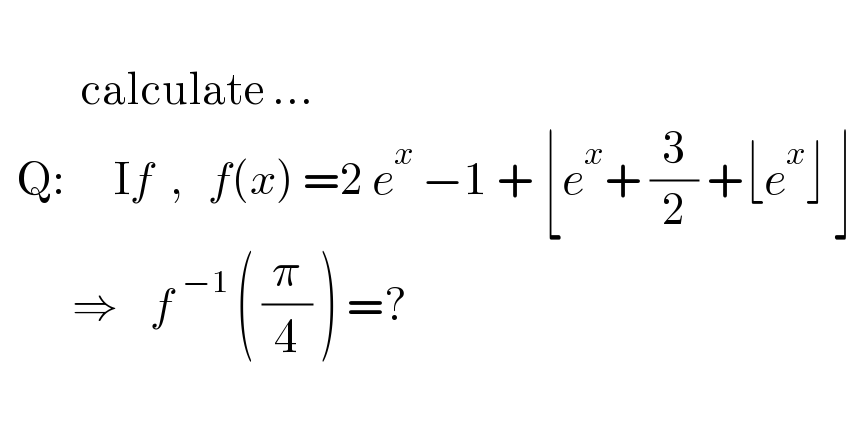
calculate ... Q: If , f(x) =2 e^x −1 + ⌊e^x + (3/2) +⌊e^x ⌋ ⌋ ⇒ f^(−1) ( (π/4) ) =?

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{calculate}\:... \\ $$$$\:\:\mathrm{Q}:\:\:\:\:\:\:\mathrm{I}{f}\:\:,\:\:\:{f}\left({x}\right)\:=\mathrm{2}\:{e}^{{x}} \:−\mathrm{1}\:+\:\lfloor{e}^{{x}} +\:\frac{\mathrm{3}}{\mathrm{2}}\:+\lfloor{e}^{{x}} \rfloor\:\rfloor \\ $$$$\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\:{f}\:^{−\mathrm{1}} \:\left(\:\frac{\pi}{\mathrm{4}}\:\right)\:=? \\ $$$$\:\:\:\:\: \\ $$

Answered by Frix last updated on 03/Nov/23

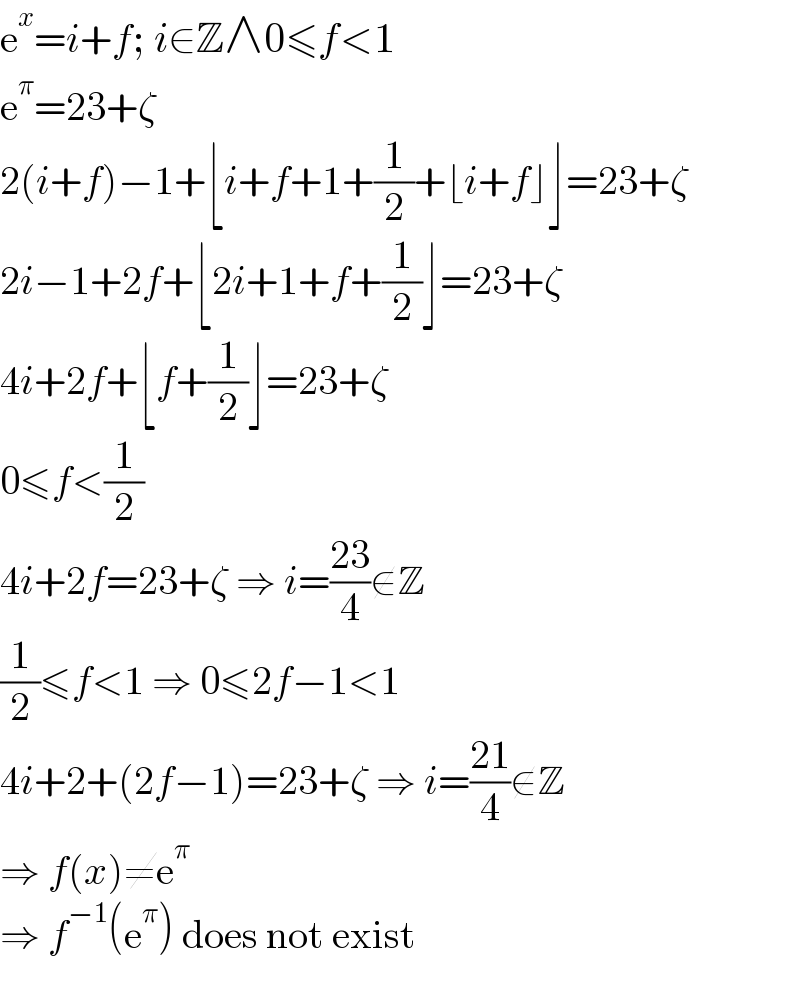
e^x =i+f; i∈Z∧0≤f<1 e^π =23+ζ 2(i+f)−1+⌊i+f+1+(1/2)+⌊i+f⌋⌋=23+ζ 2i−1+2f+⌊2i+1+f+(1/2)⌋=23+ζ 4i+2f+⌊f+(1/2)⌋=23+ζ 0≤f<(1/2) 4i+2f=23+ζ ⇒ i=((23)/4)∉Z (1/2)≤f<1 ⇒ 0≤2f−1<1 4i+2+(2f−1)=23+ζ ⇒ i=((21)/4)∉Z ⇒ f(x)≠e^π ⇒ f^(−1) (e^π ) does not exist

$$\mathrm{e}^{{x}} ={i}+{f};\:{i}\in\mathbb{Z}\wedge\mathrm{0}\leqslant{f}<\mathrm{1} \\ $$$$\mathrm{e}^{\pi} =\mathrm{23}+\zeta \\ $$$$\mathrm{2}\left({i}+{f}\right)−\mathrm{1}+\lfloor{i}+{f}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\lfloor{i}+{f}\rfloor\rfloor=\mathrm{23}+\zeta \\ $$$$\mathrm{2}{i}−\mathrm{1}+\mathrm{2}{f}+\lfloor\mathrm{2}{i}+\mathrm{1}+{f}+\frac{\mathrm{1}}{\mathrm{2}}\rfloor=\mathrm{23}+\zeta \\ $$$$\mathrm{4}{i}+\mathrm{2}{f}+\lfloor{f}+\frac{\mathrm{1}}{\mathrm{2}}\rfloor=\mathrm{23}+\zeta \\ $$$$\mathrm{0}\leqslant{f}<\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{4}{i}+\mathrm{2}{f}=\mathrm{23}+\zeta\:\Rightarrow\:{i}=\frac{\mathrm{23}}{\mathrm{4}}\notin\mathbb{Z} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\leqslant{f}<\mathrm{1}\:\Rightarrow\:\mathrm{0}\leqslant\mathrm{2}{f}−\mathrm{1}<\mathrm{1} \\ $$$$\mathrm{4}{i}+\mathrm{2}+\left(\mathrm{2}{f}−\mathrm{1}\right)=\mathrm{23}+\zeta\:\Rightarrow\:{i}=\frac{\mathrm{21}}{\mathrm{4}}\notin\mathbb{Z} \\ $$$$\Rightarrow\:{f}\left({x}\right)\neq\mathrm{e}^{\pi} \\ $$$$\Rightarrow\:{f}^{−\mathrm{1}} \left(\mathrm{e}^{\pi} \right)\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist} \\ $$

Commented by Frix last updated on 03/Nov/23

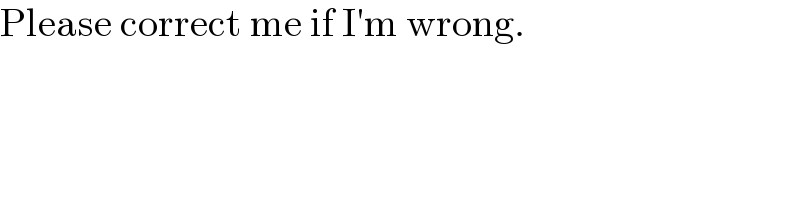
Please correct me if I′m wrong.

$$\mathrm{Please}\:\mathrm{correct}\:\mathrm{me}\:\mathrm{if}\:\mathrm{I}'\mathrm{m}\:\mathrm{wrong}. \\ $$

Commented by mnjuly1970 last updated on 03/Nov/23

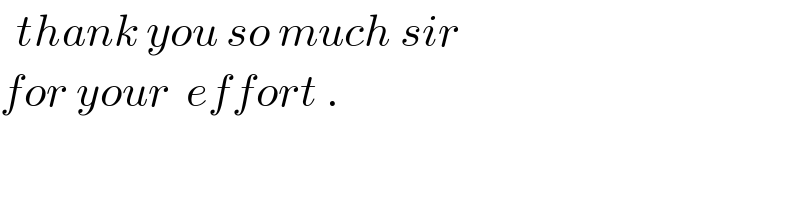
thank you so much sir for your effort .

$$\:\:{thank}\:{you}\:{so}\:{much}\:{sir} \\ $$$${for}\:{your}\:\:{effort}\:. \\ $$

Answered by mnjuly1970 last updated on 03/Nov/23

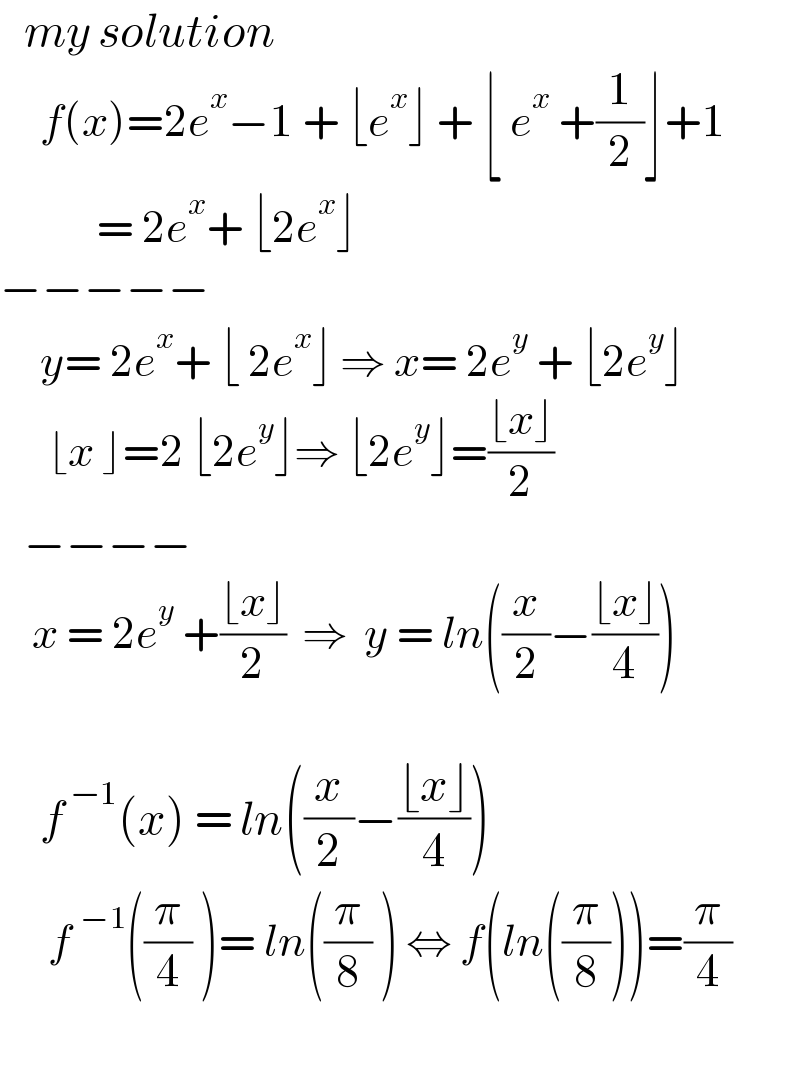
my solution f(x)=2e^x −1 + ⌊e^x ⌋ + ⌊ e^x +(1/2)⌋+1 = 2e^x + ⌊2e^x ⌋ −−−−− y= 2e^x + ⌊ 2e^x ⌋ ⇒ x= 2e^y + ⌊2e^y ⌋ ⌊x ⌋=2 ⌊2e^y ⌋⇒ ⌊2e^y ⌋=((⌊x⌋)/2) −−−− x = 2e^y +((⌊x⌋)/2) ⇒ y = ln((x/2)−((⌊x⌋)/4)) f^( −1) (x) = ln((x/2)−((⌊x⌋)/4)) f^(−1) ((π/4) )= ln((π/8) ) ⇔ f(ln((π/8)))=(π/4)

$$\:\:\:{my}\:{solution} \\ $$$$\:\:\:\:\:{f}\left({x}\right)=\mathrm{2}{e}^{{x}} −\mathrm{1}\:+\:\lfloor{e}^{{x}} \rfloor\:+\:\lfloor\:{e}^{{x}} \:+\frac{\mathrm{1}}{\mathrm{2}}\rfloor+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}{e}^{{x}} +\:\lfloor\mathrm{2}{e}^{{x}} \rfloor \\ $$$$−−−−− \\ $$$$\:\:\:\:\:{y}=\:\mathrm{2}{e}^{{x}} +\:\lfloor\:\mathrm{2}{e}^{{x}} \rfloor\:\Rightarrow\:{x}=\:\mathrm{2}{e}^{{y}} \:+\:\lfloor\mathrm{2}{e}^{{y}} \rfloor \\ $$$$\:\:\:\:\:\:\lfloor{x}\:\rfloor=\mathrm{2}\:\lfloor\mathrm{2}{e}^{{y}} \rfloor\Rightarrow\:\lfloor\mathrm{2}{e}^{{y}} \rfloor=\frac{\lfloor{x}\rfloor}{\mathrm{2}} \\ $$$$\:\:\:−−−− \\ $$$$\:\:\:\:{x}\:=\:\mathrm{2}{e}^{{y}} \:+\frac{\lfloor{x}\rfloor}{\mathrm{2}}\:\:\Rightarrow\:\:{y}\:=\:{ln}\left(\frac{{x}}{\mathrm{2}}−\frac{\lfloor{x}\rfloor}{\mathrm{4}}\right) \\ $$$$ \\ $$$$\:\:\:\:\:{f}^{\:−\mathrm{1}} \left({x}\right)\:=\:{ln}\left(\frac{{x}}{\mathrm{2}}−\frac{\lfloor{x}\rfloor}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:{f}\:^{−\mathrm{1}} \left(\frac{\pi}{\mathrm{4}}\:\right)=\:{ln}\left(\frac{\pi}{\mathrm{8}}\:\right)\:\Leftrightarrow\:{f}\left({ln}\left(\frac{\pi}{\mathrm{8}}\right)\right)=\frac{\pi}{\mathrm{4}} \\ $$$$\:\: \\ $$

Commented by Frix last updated on 03/Nov/23

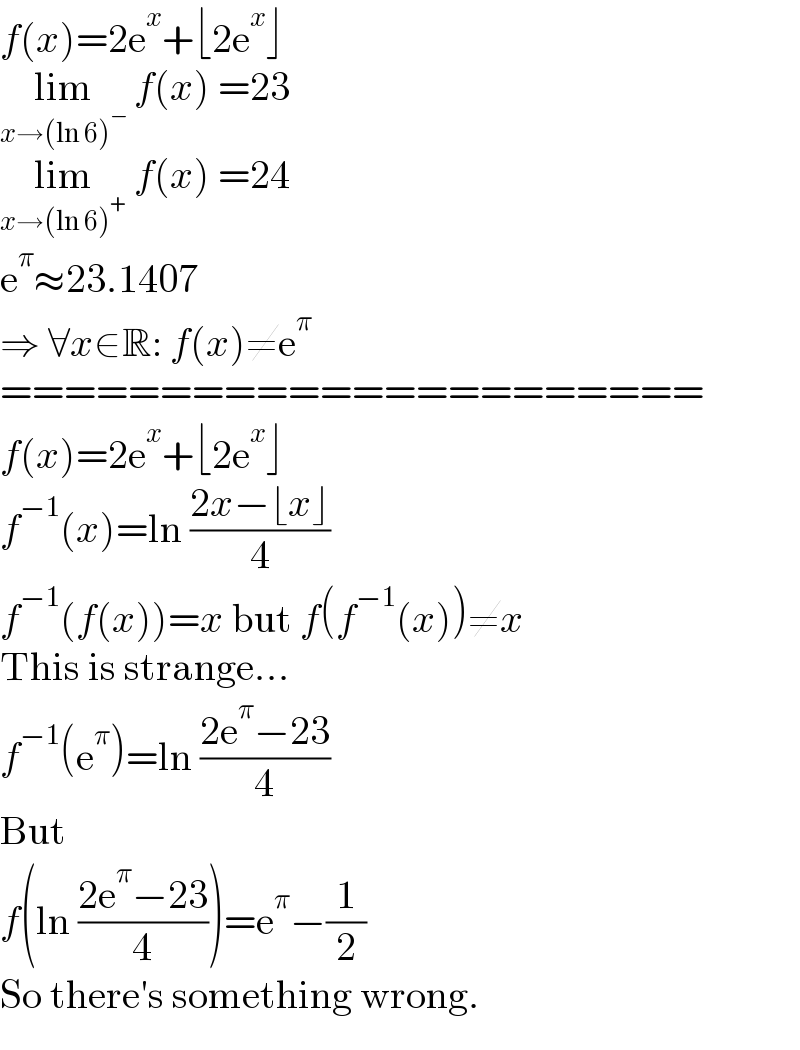
f(x)=2e^x +⌊2e^x ⌋ lim_(x→(ln 6)^− ) f(x) =23 lim_(x→(ln 6)^+ ) f(x) =24 e^π ≈23.1407 ⇒ ∀x∈R: f(x)≠e^π ====================== f(x)=2e^x +⌊2e^x ⌋ f^(−1) (x)=ln ((2x−⌊x⌋)/4) f^(−1) (f(x))=x but f(f^(−1) (x))≠x This is strange... f^(−1) (e^π )=ln ((2e^π −23)/4) But f(ln ((2e^π −23)/4))=e^π −(1/2) So there′s something wrong.

$${f}\left({x}\right)=\mathrm{2e}^{{x}} +\lfloor\mathrm{2e}^{{x}} \rfloor \\ $$$$\underset{{x}\rightarrow\left(\mathrm{ln}\:\mathrm{6}\right)^{−} } {\mathrm{lim}}\:{f}\left({x}\right)\:=\mathrm{23} \\ $$$$\underset{{x}\rightarrow\left(\mathrm{ln}\:\mathrm{6}\right)^{+} } {\mathrm{lim}}\:{f}\left({x}\right)\:=\mathrm{24} \\ $$$$\mathrm{e}^{\pi} \approx\mathrm{23}.\mathrm{1407} \\ $$$$\Rightarrow\:\forall{x}\in\mathbb{R}:\:{f}\left({x}\right)\neq\mathrm{e}^{\pi} \\ $$$$====================== \\ $$$${f}\left({x}\right)=\mathrm{2e}^{{x}} +\lfloor\mathrm{2e}^{{x}} \rfloor \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\mathrm{ln}\:\frac{\mathrm{2}{x}−\lfloor{x}\rfloor}{\mathrm{4}} \\ $$$${f}^{−\mathrm{1}} \left({f}\left({x}\right)\right)={x}\:\mathrm{but}\:{f}\left({f}^{−\mathrm{1}} \left({x}\right)\right)\neq{x} \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{strange}...\: \\ $$$${f}^{−\mathrm{1}} \left(\mathrm{e}^{\pi} \right)=\mathrm{ln}\:\frac{\mathrm{2e}^{\pi} −\mathrm{23}}{\mathrm{4}} \\ $$$$\mathrm{But} \\ $$$${f}\left(\mathrm{ln}\:\frac{\mathrm{2e}^{\pi} −\mathrm{23}}{\mathrm{4}}\right)=\mathrm{e}^{\pi} −\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{So}\:\mathrm{there}'\mathrm{s}\:\mathrm{something}\:\mathrm{wrong}. \\ $$

Commented by Frix last updated on 03/Nov/23

v=u+⌊u⌋ The range of this function is R\{v∈R∧n∈Z∣2n−1≤v<2n} ⇒ v^(−1) is not defined in these intervals ⇒ f^(−1) (x)= { ((ln ((2x−⌊x⌋)/4), 2n≤x<2n+1)),((undefined, 2n−1≤x<2n)) :} ∀n∈Z 23<e^π <24 2×12−1<e^π <2×12 ⇒ f^(−1) (e^π ) doesn′t exist

$${v}={u}+\lfloor{u}\rfloor \\ $$$$\mathrm{The}\:\mathrm{range}\:\mathrm{of}\:\mathrm{this}\:\mathrm{function}\:\mathrm{is} \\ $$$$\mathbb{R}\backslash\left\{{v}\in\mathbb{R}\wedge{n}\in\mathbb{Z}\mid\mathrm{2}{n}−\mathrm{1}\leqslant{v}<\mathrm{2}{n}\right\} \\ $$$$\Rightarrow\:{v}^{−\mathrm{1}} \:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{in}\:\mathrm{these}\:\mathrm{intervals} \\ $$$$\Rightarrow \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\begin{cases}{\mathrm{ln}\:\frac{\mathrm{2}{x}−\lfloor{x}\rfloor}{\mathrm{4}},\:\mathrm{2}{n}\leqslant{x}<\mathrm{2}{n}+\mathrm{1}}\\{\mathrm{undefined},\:\mathrm{2}{n}−\mathrm{1}\leqslant{x}<\mathrm{2}{n}}\end{cases}\:\forall{n}\in\mathbb{Z} \\ $$$$\mathrm{23}<\mathrm{e}^{\pi} <\mathrm{24} \\ $$$$\mathrm{2}×\mathrm{12}−\mathrm{1}<\mathrm{e}^{\pi} <\mathrm{2}×\mathrm{12} \\ $$$$\Rightarrow \\ $$$${f}^{−\mathrm{1}} \left(\mathrm{e}^{\pi} \right)\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$

Commented by mnjuly1970 last updated on 03/Nov/23

thanks alot sir.you are right ⋛

$${thanks}\:{alot}\:{sir}.{you}\:{are}\:{right}\:\underline{\underbrace{\lesseqgtr}} \\ $$

Commented by Frix last updated on 03/Nov/23

You′re welcome, working on these things keeps my brain young.

$$\mathrm{You}'\mathrm{re}\:\mathrm{welcome},\:\mathrm{working}\:\mathrm{on}\:\mathrm{these}\:\mathrm{things} \\ $$$$\mathrm{keeps}\:\mathrm{my}\:\mathrm{brain}\:\mathrm{young}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com