
Question Number 199393 by Calculusboy last updated on 02/Nov/23
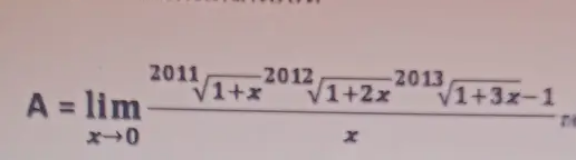
Answered by cortano12 last updated on 03/Nov/23
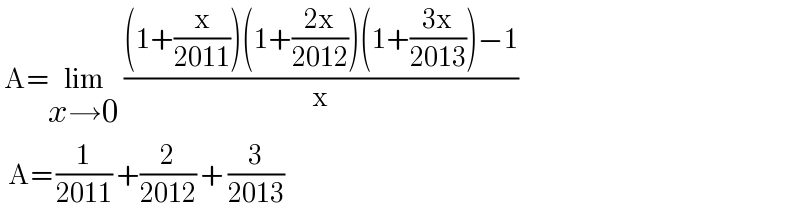
$$\:\mathrm{A}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{2011}}\right)\left(\mathrm{1}+\frac{\mathrm{2x}}{\mathrm{2012}}\right)\left(\mathrm{1}+\frac{\mathrm{3x}}{\mathrm{2013}}\right)−\mathrm{1}}{\mathrm{x}} \\ $$$$\:\:\mathrm{A}=\:\frac{\mathrm{1}}{\mathrm{2011}}\:+\frac{\mathrm{2}}{\mathrm{2012}}\:+\:\frac{\mathrm{3}}{\mathrm{2013}}\: \\ $$
Commented by essaad last updated on 03/Nov/23
hi sir Can you explain to us how you did that?
Commented by MathematicalUser2357 last updated on 03/Nov/23

$$ \\ $$Calculator???
Answered by mr W last updated on 03/Nov/23
![((1+x))^(1/(2011)) =(1+x)^(1/(2011)) =1+(x/(2011))+terms with x^2 or higher =1+(x/(2011))+o(x^2 ) similarly ((1+2x))^(1/(2012)) =1+((2x)/(2012))+o(x^2 ) ((1+3x))^(1/(2013)) =1+((3x)/(2013))+o(x^2 ) ((1+x))^(1/(2011)) ×((1+2x))^(1/(2012)) ×((1+3x))^(1/(2013)) =[1+(x/(2011))+o(x^2 )][1+((2x)/(2012))+o(x^2 )][1+((3x)/(2013))+o(x^2 )] =1+((1/(2011))+(2/(2012))+(3/(2013)))x+o(x^2 ) ((((1+x))^(1/(2011)) ×((1+2x))^(1/(2012)) ×((1+3x))^(1/(2013)) −1)/x) =((1/(2011))+(2/(2012))+(3/(2013)))+o(x) lim_(x→0) ((((1+x))^(1/(2011)) ×((1+2x))^(1/(2012)) ×((1+3x))^(1/(2013)) −1)/x) =lim_(x→0) [((1/(2011))+(2/(2012))+(3/(2013)))+o(x)] =(1/(2011))+(2/(2012))+(3/(2013))+lim_(x→0) o(x) =(1/(2011))+(2/(2012))+(3/(2013))+0 =(1/(2011))+(2/(2012))+(3/(2013))](Q199401.png)
$$\sqrt[{\mathrm{2011}}]{\mathrm{1}+{x}}=\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{2011}}} =\mathrm{1}+\frac{{x}}{\mathrm{2011}}+{terms}\:{with}\:{x}^{\mathrm{2}} \:{or}\:{higher} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\frac{{x}}{\mathrm{2011}}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$${similarly} \\ $$$$\sqrt[{\mathrm{2012}}]{\mathrm{1}+\mathrm{2}{x}}=\mathrm{1}+\frac{\mathrm{2}{x}}{\mathrm{2012}}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$\sqrt[{\mathrm{2013}}]{\mathrm{1}+\mathrm{3}{x}}=\mathrm{1}+\frac{\mathrm{3}{x}}{\mathrm{2013}}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$ \\ $$$$\sqrt[{\mathrm{2011}}]{\mathrm{1}+{x}}×\sqrt[{\mathrm{2012}}]{\mathrm{1}+\mathrm{2}{x}}×\sqrt[{\mathrm{2013}}]{\mathrm{1}+\mathrm{3}{x}} \\ $$$$=\left[\mathrm{1}+\frac{{x}}{\mathrm{2011}}+{o}\left({x}^{\mathrm{2}} \right)\right]\left[\mathrm{1}+\frac{\mathrm{2}{x}}{\mathrm{2012}}+{o}\left({x}^{\mathrm{2}} \right)\right]\left[\mathrm{1}+\frac{\mathrm{3}{x}}{\mathrm{2013}}+{o}\left({x}^{\mathrm{2}} \right)\right] \\ $$$$=\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{2011}}+\frac{\mathrm{2}}{\mathrm{2012}}+\frac{\mathrm{3}}{\mathrm{2013}}\right){x}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$ \\ $$$$\frac{\sqrt[{\mathrm{2011}}]{\mathrm{1}+{x}}×\sqrt[{\mathrm{2012}}]{\mathrm{1}+\mathrm{2}{x}}×\sqrt[{\mathrm{2013}}]{\mathrm{1}+\mathrm{3}{x}}−\mathrm{1}}{{x}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2011}}+\frac{\mathrm{2}}{\mathrm{2012}}+\frac{\mathrm{3}}{\mathrm{2013}}\right)+{o}\left({x}\right) \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{2011}}]{\mathrm{1}+{x}}×\sqrt[{\mathrm{2012}}]{\mathrm{1}+\mathrm{2}{x}}×\sqrt[{\mathrm{2013}}]{\mathrm{1}+\mathrm{3}{x}}−\mathrm{1}}{{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\frac{\mathrm{1}}{\mathrm{2011}}+\frac{\mathrm{2}}{\mathrm{2012}}+\frac{\mathrm{3}}{\mathrm{2013}}\right)+{o}\left({x}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2011}}+\frac{\mathrm{2}}{\mathrm{2012}}+\frac{\mathrm{3}}{\mathrm{2013}}+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{o}\left({x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2011}}+\frac{\mathrm{2}}{\mathrm{2012}}+\frac{\mathrm{3}}{\mathrm{2013}}+\mathrm{0} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2011}}+\frac{\mathrm{2}}{\mathrm{2012}}+\frac{\mathrm{3}}{\mathrm{2013}} \\ $$
Commented by Calculusboy last updated on 03/Nov/23

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$
