Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 198210 by a.lgnaoui last updated on 14/Oct/23

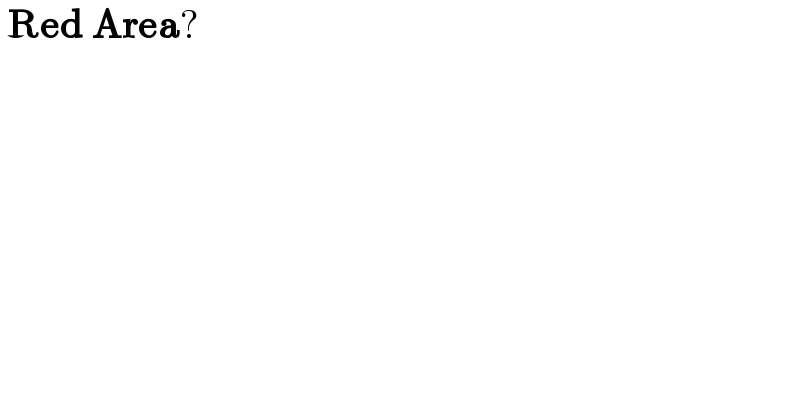
Red Area?

$$\:\boldsymbol{\mathrm{Red}}\:\boldsymbol{\mathrm{Area}}? \\ $$

Commented by a.lgnaoui last updated on 14/Oct/23

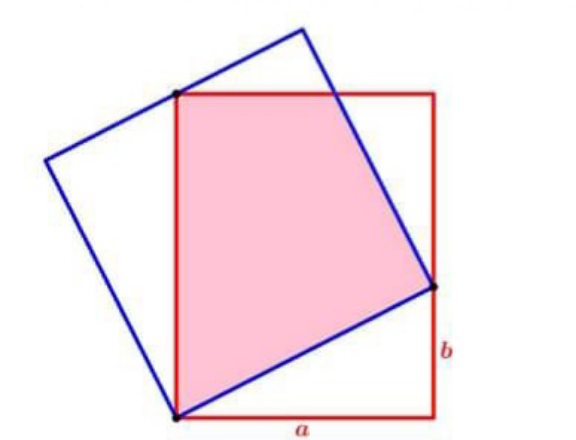
Answered by mr W last updated on 14/Oct/23

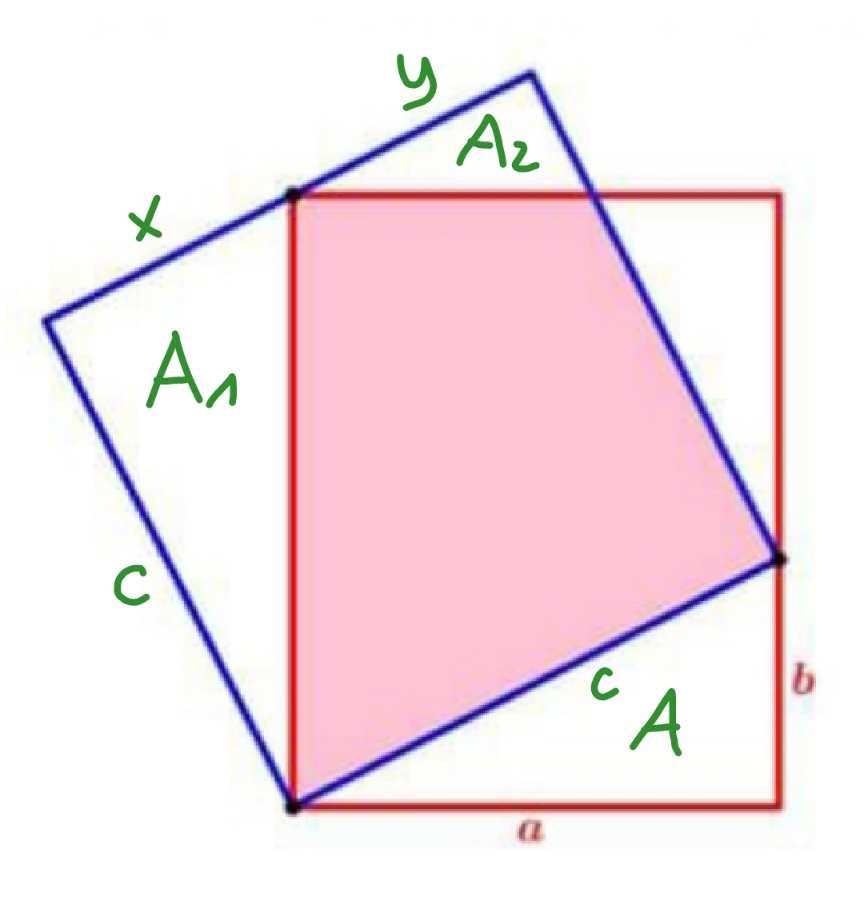
Commented by mr W last updated on 14/Oct/23

c=(√(a^2 +b^2 )) A=((ab)/2) (A_1 /A)=((c/a))^2 ⇒A_1 =(c^2 /a^2 )A (x/c)=(b/a) ⇒x=((bc)/a) y=c−x=c−((bc)/a)=(1−(b/a))c (A_2 /A)=((y/a))^2 ⇒A_2 =(1−(b/a))^2 (c^2 /a^2 )A A_1 +A_2 =[1+(1−(b/a))^2 ]((a^2 +b^2 )/a^2 )×((ab)/2) A_1 +A_2 =(((a^2 +b^2 )(2a^2 +b^2 −2ab)b)/(2a^3 )) A_(shaded) =c^2 −A_1 −A_2 =a^2 +b^2 −(((a^2 +b^2 )(2a^2 +b^2 −2ab)b)/(2a^3 )) A_(shaded) =(((a^2 +b^2 )(2a^3 −2a^2 b+2ab^2 −b^3 ))/(2a^3 )) ✓

$${c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${A}=\frac{{ab}}{\mathrm{2}} \\ $$$$\frac{{A}_{\mathrm{1}} }{{A}}=\left(\frac{{c}}{{a}}\right)^{\mathrm{2}} \:\Rightarrow{A}_{\mathrm{1}} =\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{A} \\ $$$$\frac{{x}}{{c}}=\frac{{b}}{{a}}\:\Rightarrow{x}=\frac{{bc}}{{a}} \\ $$$${y}={c}−{x}={c}−\frac{{bc}}{{a}}=\left(\mathrm{1}−\frac{{b}}{{a}}\right){c} \\ $$$$\frac{{A}_{\mathrm{2}} }{{A}}=\left(\frac{{y}}{{a}}\right)^{\mathrm{2}} \:\Rightarrow{A}_{\mathrm{2}} =\left(\mathrm{1}−\frac{{b}}{{a}}\right)^{\mathrm{2}} \frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{A} \\ $$$${A}_{\mathrm{1}} +{A}_{\mathrm{2}} =\left[\mathrm{1}+\left(\mathrm{1}−\frac{{b}}{{a}}\right)^{\mathrm{2}} \right]\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }×\frac{{ab}}{\mathrm{2}} \\ $$$${A}_{\mathrm{1}} +{A}_{\mathrm{2}} =\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{2}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\right){b}}{\mathrm{2}{a}^{\mathrm{3}} } \\ $$$${A}_{{shaded}} ={c}^{\mathrm{2}} −{A}_{\mathrm{1}} −{A}_{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{2}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\right){b}}{\mathrm{2}{a}^{\mathrm{3}} } \\ $$$${A}_{{shaded}} =\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{2}{a}^{\mathrm{3}} −\mathrm{2}{a}^{\mathrm{2}} {b}+\mathrm{2}{ab}^{\mathrm{2}} −{b}^{\mathrm{3}} \right)}{\mathrm{2}{a}^{\mathrm{3}} }\:\checkmark \\ $$

Commented by a.lgnaoui last updated on 14/Oct/23

thanks

$$\mathrm{thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com