Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 198059 by a.lgnaoui last updated on 09/Oct/23

Montrer l egalite (voir la figure )

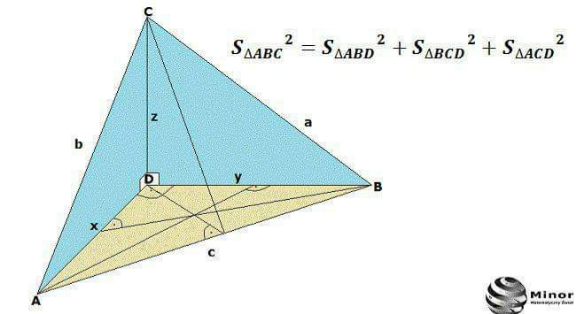
$$\mathrm{Montrer}\:\mathrm{l}\:\mathrm{egalite}\:\:\left(\mathrm{voir}\:\mathrm{la}\:\mathrm{figure}\:\right) \\ $$

Commented by a.lgnaoui last updated on 09/Oct/23

Answered by mr W last updated on 10/Oct/23

a^2 =z^2 +y^2 b^2 =x^2 +z^2 c^2 =y^2 +x^2 ΔABC=((√((a^2 +b^2 +c^2 )^2 −2(a^4 +b^4 +c^4 )))/4) ΔABC^2 =(((a^2 +b^2 +c^2 )^2 −2(a^4 +b^4 +c^4 ))/(16)) ΔABC^2 =((4(x^2 +y^2 +z^2 )^2 −2(x^4 +y^4 +2x^2 y^2 +y^4 +z^4 +2y^2 z^2 +z^4 +x^4 +2z^2 x^2 ))/(16)) ΔABC^2 =(((x^2 +y^2 +z^2 )^2 −(x^4 +y^4 +z^4 +x^2 y^2 +y^2 z^2 +z^2 x^2 ))/4) ΔABC^2 =((x^2 y^2 +y^2 z^2 +z^2 x^2 )/4) ΔABC^2 =(((xy)/2))^2 +(((yz)/2))^2 +(((zx)/2))^2 ⇒ΔABC^2 =ΔABD^2 +ΔBCD^2 +ΔACD^2 ✓

$${a}^{\mathrm{2}} ={z}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} ={x}^{\mathrm{2}} +{z}^{\mathrm{2}} \\ $$$${c}^{\mathrm{2}} ={y}^{\mathrm{2}} +{x}^{\mathrm{2}} \\ $$$$\Delta{ABC}=\frac{\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)}}{\mathrm{4}} \\ $$$$\Delta{ABC}^{\mathrm{2}} =\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)}{\mathrm{16}} \\ $$$$\Delta{ABC}^{\mathrm{2}} =\frac{\mathrm{4}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left({x}^{\mathrm{4}} +{y}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +\mathrm{2}{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{4}} +{x}^{\mathrm{4}} +\mathrm{2}{z}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}{\mathrm{16}} \\ $$$$\Delta{ABC}^{\mathrm{2}} =\frac{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{2}} −\left({x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}{\mathrm{4}} \\ $$$$\Delta{ABC}^{\mathrm{2}} =\frac{{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Delta{ABC}^{\mathrm{2}} =\left(\frac{{xy}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{yz}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{zx}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\Delta{ABC}^{\mathrm{2}} =\Delta{ABD}^{\mathrm{2}} +\Delta{BCD}^{\mathrm{2}} +\Delta{ACD}^{\mathrm{2}} \:\checkmark \\ $$

Commented by a.lgnaoui last updated on 09/Oct/23

thanks

$$\mathrm{thanks}\: \\ $$

Commented by a.lgnaoui last updated on 09/Oct/23

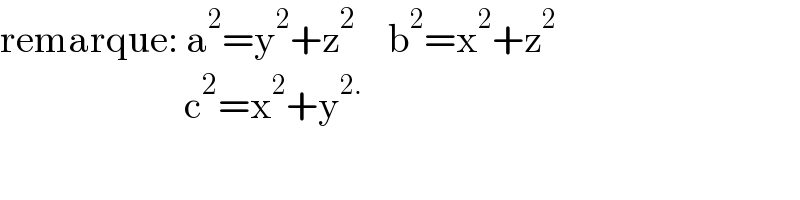
remarque: a^2 =y^2 +z^2 b^2 =x^2 +z^2 c^2 =x^2 +y^(2.)

$$\mathrm{remarque}:\:\mathrm{a}^{\mathrm{2}} =\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \:\:\:\:\mathrm{b}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{c}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}.} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com