
Question Number 197947 by mnjuly1970 last updated on 05/Oct/23
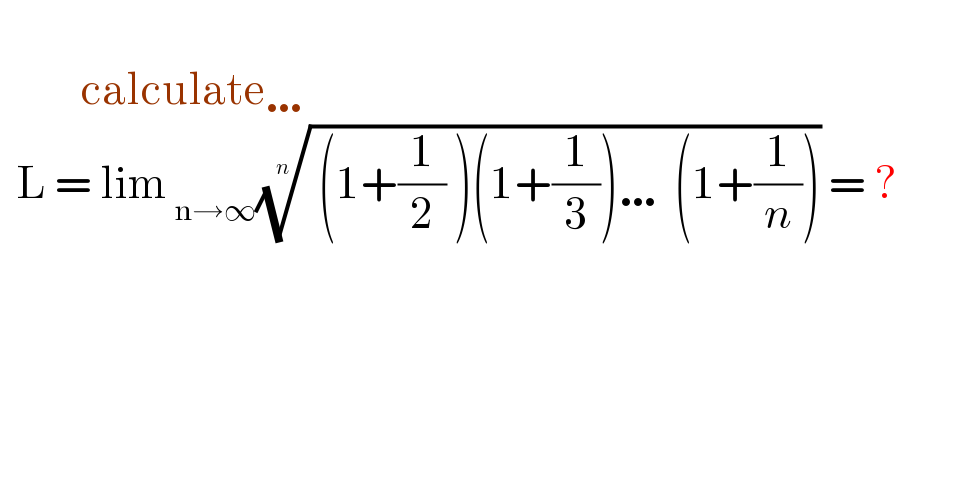
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{calculate}\ldots \\ $$$$\:\:\mathrm{L}\:=\:\mathrm{lim}\:_{\mathrm{n}\rightarrow\infty} \sqrt[{{n}}]{\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)\ldots\:\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)}\:=\:?\:\:\:\:\:\:\:\: \\ $$$$\:\: \\ $$
Answered by MM42 last updated on 05/Oct/23
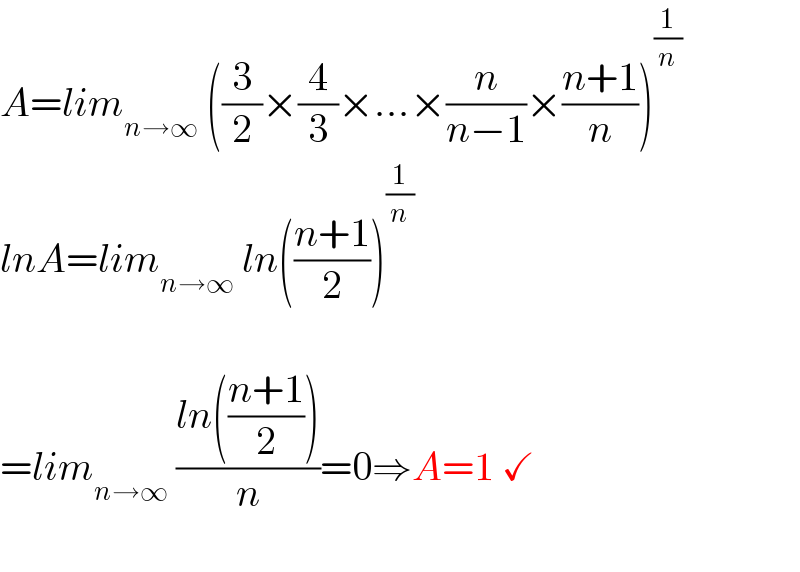
$${A}={lim}_{{n}\rightarrow\infty} \:\left(\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{3}}×...×\frac{{n}}{{n}−\mathrm{1}}×\frac{{n}+\mathrm{1}}{{n}}\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$${lnA}={lim}_{{n}\rightarrow\infty} \:{ln}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$ \\ $$$$={lim}_{{n}\rightarrow\infty} \:\frac{{ln}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)}{{n}}=\mathrm{0}\Rightarrow{A}=\mathrm{1}\:\checkmark \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 05/Oct/23

$${thx}\:{alot}\:{sir}\:... \\ $$
