
Question Number 197920 by cortano12 last updated on 04/Oct/23
Commented by cortano12 last updated on 04/Oct/23

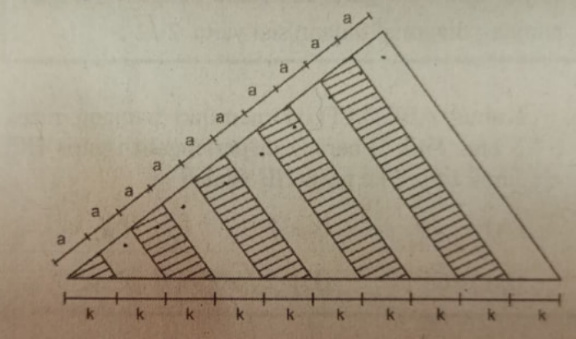
$$\mathrm{if}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{is}\:\mathrm{320}\:\mathrm{cm}^{\mathrm{2}} \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{big}\:\mathrm{triangle}.\: \\ $$
Answered by Tokugami last updated on 04/Oct/23
![shaded area is 320 cm^2 first n triangles area: A((n/(10)))^2 =(A/(100))n^2 nth wedge area=(A/(100))(n^2 −(n−1)^2 )=(A/(100))(2n−1) (A/(100))[(2(9)−1)+(2(7)−1)+(2(5)−1)+(2(3)−1)+(2(1)−1)]=320 (A/(100))(17+13+9+5+1)=320 ((45A)/(100))=320 A=((6400)/9) cm^2 =711.11 cm^2](Q197924.png)
$$\mathrm{shaded}\:\mathrm{area}\:\mathrm{is}\:\mathrm{320}\:\mathrm{cm}^{\mathrm{2}} \\ $$$$\mathrm{first}\:{n}\:\mathrm{triangles}\:\mathrm{area}:\:{A}\left(\frac{{n}}{\mathrm{10}}\right)^{\mathrm{2}} =\frac{{A}}{\mathrm{100}}{n}^{\mathrm{2}} \\ $$$$\mathrm{nth}\:\mathrm{wedge}\:\mathrm{area}=\frac{{A}}{\mathrm{100}}\left({n}^{\mathrm{2}} −\left({n}−\mathrm{1}\right)^{\mathrm{2}} \right)=\frac{{A}}{\mathrm{100}}\left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$$\frac{{A}}{\mathrm{100}}\left[\left(\mathrm{2}\left(\mathrm{9}\right)−\mathrm{1}\right)+\left(\mathrm{2}\left(\mathrm{7}\right)−\mathrm{1}\right)+\left(\mathrm{2}\left(\mathrm{5}\right)−\mathrm{1}\right)+\left(\mathrm{2}\left(\mathrm{3}\right)−\mathrm{1}\right)+\left(\mathrm{2}\left(\mathrm{1}\right)−\mathrm{1}\right)\right]=\mathrm{320} \\ $$$$\frac{{A}}{\mathrm{100}}\left(\mathrm{17}+\mathrm{13}+\mathrm{9}+\mathrm{5}+\mathrm{1}\right)=\mathrm{320} \\ $$$$\frac{\mathrm{45}{A}}{\mathrm{100}}=\mathrm{320} \\ $$$${A}=\frac{\mathrm{6400}}{\mathrm{9}}\:\mathrm{cm}^{\mathrm{2}} =\mathrm{711}.\mathrm{11}\:\mathrm{cm}^{\mathrm{2}} \\ $$$$ \\ $$
Answered by Sutrisno last updated on 14/Oct/23

$$ \\ $$
