
Question Number 19792 by Tinkutara last updated on 15/Aug/17

$$\mathrm{Let}\:{ABCD}\:\mathrm{be}\:\mathrm{a}\:\mathrm{convex}\:\mathrm{quadrilateral} \\ $$$$\mathrm{with}\:\angle{DAB}\:=\:\angle{BDC}\:=\:\mathrm{90}°.\:\mathrm{Let}\:\mathrm{the} \\ $$$$\mathrm{incircles}\:\mathrm{of}\:\mathrm{triangles}\:{ABD}\:\mathrm{and}\:{BCD} \\ $$$$\mathrm{touch}\:{BD}\:\mathrm{at}\:{P}\:\mathrm{and}\:{Q},\:\mathrm{respectively}, \\ $$$$\mathrm{with}\:{P}\:\mathrm{lying}\:\mathrm{in}\:\mathrm{between}\:{B}\:\mathrm{and}\:{Q}.\:\mathrm{If} \\ $$$${AD}\:=\:\mathrm{999}\:\mathrm{and}\:{PQ}\:=\:\mathrm{200}\:\mathrm{then}\:\mathrm{what}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{radii}\:\mathrm{of}\:\mathrm{the}\:\mathrm{incircles}\:\mathrm{of} \\ $$$$\mathrm{triangles}\:{ABD}\:\mathrm{and}\:{BDC}? \\ $$
Answered by ajfour last updated on 16/Aug/17
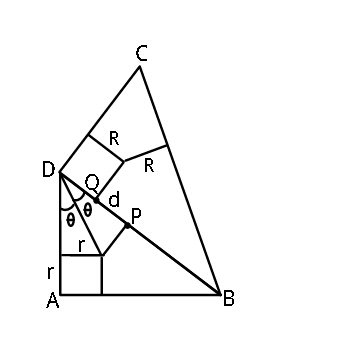
Commented by ajfour last updated on 16/Aug/17
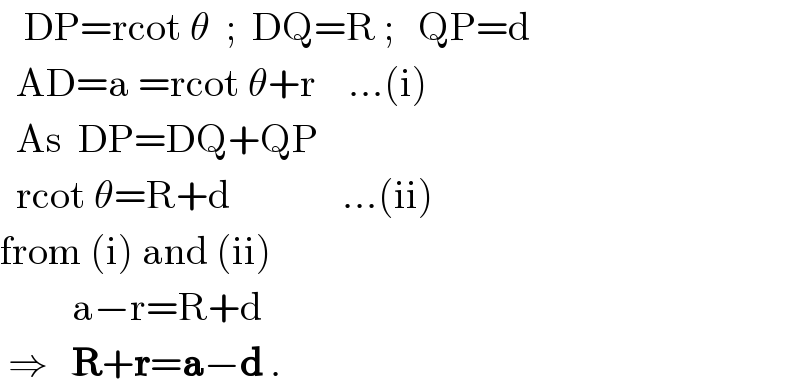
$$\:\:\:\mathrm{DP}=\mathrm{rcot}\:\theta\:\:;\:\:\mathrm{DQ}=\mathrm{R}\:;\:\:\:\mathrm{QP}=\mathrm{d} \\ $$$$\:\:\mathrm{AD}=\mathrm{a}\:=\mathrm{rcot}\:\theta+\mathrm{r}\:\:\:\:...\left(\mathrm{i}\right) \\ $$$$\:\:\mathrm{As}\:\:\mathrm{DP}=\mathrm{DQ}+\mathrm{QP} \\ $$$$\:\:\mathrm{rcot}\:\theta=\mathrm{R}+\mathrm{d}\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\left(\mathrm{ii}\right) \\ $$$$\mathrm{from}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{a}−\mathrm{r}=\mathrm{R}+\mathrm{d} \\ $$$$\:\Rightarrow\:\:\:\boldsymbol{\mathrm{R}}+\boldsymbol{\mathrm{r}}=\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{d}}\:. \\ $$
Commented by Tinkutara last updated on 16/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Answered by ajfour last updated on 16/Aug/17

$$\:\:\mathrm{R}+\mathrm{r}=\mathrm{AD}−\mathrm{PQ}\:. \\ $$
