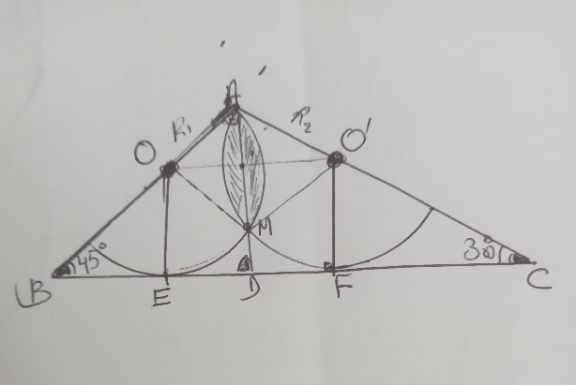
Question Number 197914 by a.lgnaoui last updated on 04/Oct/23

$$\boldsymbol{\mathrm{Determiner}}\:\boldsymbol{\mathrm{la}}\:\boldsymbol{\mathrm{surface}}\:\boldsymbol{\mathrm{hachuree}} \\ $$$$\left(\boldsymbol{\mathrm{voir}}\:\:\boldsymbol{\mathrm{figure}}\right) \\ $$$$\:\boldsymbol{\mathrm{BC}}=\mathrm{10}\boldsymbol{\mathrm{cm}}\:\:\:\:\:\measuredangle\boldsymbol{\mathrm{B}}=\mathrm{45}°\:\:\:\:\:\:\measuredangle\boldsymbol{\mathrm{C}}=\mathrm{30}° \\ $$
Commented by a.lgnaoui last updated on 04/Oct/23
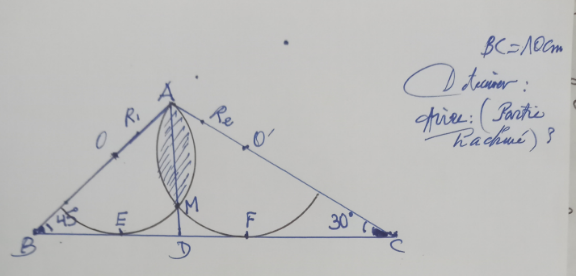
Commented by a.lgnaoui last updated on 05/Oct/23

$${Reponse}: \\ $$$$\boldsymbol{\mathrm{AB}}\mathrm{sin}\:\mathrm{45}°=\boldsymbol{\mathrm{AC}}\mathrm{sin}\:\mathrm{30}° \\ $$$$\:\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\boldsymbol{\mathrm{AB}}=\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{AC}}\:\:\:\Rightarrow\:\:\boldsymbol{\mathrm{AC}}=\boldsymbol{\mathrm{AB}}\sqrt{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{BC}}^{\mathrm{2}} =\boldsymbol{\mathrm{AB}}^{\mathrm{2}} +\boldsymbol{\mathrm{AC}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{AB}}×\boldsymbol{\mathrm{AC}}\mathrm{cos}\:\mathrm{105}° \\ $$$$\mathrm{100}=\mathrm{3AB}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\mathrm{AB}^{\mathrm{2}} \mathrm{cos}\:\mathrm{105} \\ $$$$\:\:\:\:\:\:=\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\:\mathrm{105}\right)\mathrm{AB}^{\mathrm{2}} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{AB}}=\frac{\mathrm{10}}{\:\sqrt{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{105}}} \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{AB}}=\mathrm{5},\mathrm{176} \\ $$$$\:\bullet\bigtriangleup\mathrm{OBE}\:\:\:\mathrm{sin}\:\mathrm{45}°=\frac{\boldsymbol{\mathrm{OE}}}{\boldsymbol{\mathrm{OB}}}=\frac{\boldsymbol{\mathrm{R}}\mathrm{1}}{\boldsymbol{\mathrm{AB}}−\boldsymbol{\mathrm{R}}\mathrm{1}} \\ $$$$\Rightarrow\left(\boldsymbol{\mathrm{AB}}−\boldsymbol{\mathrm{R}}\mathrm{1}\right)\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\boldsymbol{\mathrm{R}}\mathrm{1}\: \\ $$$$\:\:\:\boldsymbol{\mathrm{AB}}−\boldsymbol{\mathrm{R}}\mathrm{1}=\boldsymbol{\mathrm{R}}\mathrm{1}\sqrt{\mathrm{2}\:}\:\:\:\:\:\:\boldsymbol{\mathrm{R}}\mathrm{1}=\frac{\boldsymbol{\mathrm{AB}}}{\mathrm{1}+\sqrt{\mathrm{2}}} \\ $$$$\:\:\boldsymbol{\mathrm{R}}\mathrm{1}=\frac{\mathrm{10}}{\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right)\sqrt{\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{105}\right)}} \\ $$$$ \\ $$$$\:\:\:\:\boldsymbol{\mathrm{AN}}\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{R}}\mathrm{1}=\mathrm{2},\mathrm{14}\:\:\: \\ $$$$\:\bullet\measuredangle\boldsymbol{\mathrm{OFC}}\:\:\:\:\mathrm{sin}\:\mathrm{30}=\frac{\boldsymbol{\mathrm{R}}\mathrm{2}}{\boldsymbol{\mathrm{OC}}}=\frac{\boldsymbol{\mathrm{R}}\mathrm{2}}{\boldsymbol{\mathrm{AC}}−\boldsymbol{\mathrm{R}}\mathrm{2}} \\ $$$$\:\:\boldsymbol{\mathrm{AC}}=\boldsymbol{\mathrm{AB}}\sqrt{\mathrm{2}\:}\:\:\:\:\Rightarrow\boldsymbol{\mathrm{AC}}=\mathrm{5},\mathrm{176}×\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{AC}}=\mathrm{7},\mathrm{32} \\ $$$$\:\:\:\frac{\boldsymbol{\mathrm{AC}}}{\mathrm{2}}−\frac{\boldsymbol{\mathrm{R}}\mathrm{2}}{\mathrm{2}}=\boldsymbol{\mathrm{R}}\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{R}}\mathrm{2}=\frac{\boldsymbol{\mathrm{AC}}}{\mathrm{3}}=\mathrm{2},\mathrm{44} \\ $$$$\bullet\boldsymbol{\mathrm{Calcul}}\:\boldsymbol{\mathrm{de}}\:\boldsymbol{\mathrm{la}}\:\boldsymbol{\mathrm{surface}} \\ $$$$\boldsymbol{\mathrm{S}}=\boldsymbol{\mathrm{S}}\mathrm{1}+\boldsymbol{\mathrm{S}}\mathrm{2} \\ $$$$\:\:\boldsymbol{\mathrm{S}}\mathrm{1}=\:\:\frac{\boldsymbol{\pi\mathrm{R}}\mathrm{1}^{\mathrm{2}} ×\boldsymbol{\alpha}}{\mathrm{360}}\:\:\:\:−\boldsymbol{\mathrm{S}}\left(\bigtriangleup\boldsymbol{\mathrm{OAM}}\right) \\ $$$$\:\:\boldsymbol{\mathrm{S}}\mathrm{2}=\frac{\boldsymbol{\pi\mathrm{R}}\mathrm{2}^{\mathrm{2}} ×\boldsymbol{\beta}}{\mathrm{360}}\:−\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{AO}}'\boldsymbol{\mathrm{M}}\right)\: \\ $$$$\bigtriangleup\boldsymbol{\mathrm{AOM}}=\frac{\mathrm{sin}\:\boldsymbol{\mathrm{A}}\mathrm{1}}{\boldsymbol{\mathrm{R}}\mathrm{1}}=\frac{\mathrm{sin}\:\mathrm{2}\boldsymbol{\mathrm{A}}\mathrm{1}}{\boldsymbol{\mathrm{AM}}}\:\:\: \\ $$$$\:\:\:\:\mathrm{A1}=\alpha\:\:\:\:\Rightarrow\:\:\frac{\mathrm{sin}\:\alpha}{\boldsymbol{\mathrm{R}}\mathrm{1}}=\frac{\mathrm{sin}\:\mathrm{2}\boldsymbol{\alpha}}{\boldsymbol{\mathrm{AM}}} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{AM}}=\mathrm{2}\boldsymbol{\mathrm{R}}\mathrm{1cos}\:\boldsymbol{\alpha}\:\:\: \\ $$$$\:\:\:\:\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{OSM}}\right)=\frac{\boldsymbol{\pi\mathrm{R}}\mathrm{1}^{\mathrm{2}} }{\mathrm{360}}\boldsymbol{\alpha}−\frac{\mathrm{AM}}{\mathrm{2}}\mathrm{R1cos}\:\boldsymbol{\alpha} \\ $$$$\:\:\:\:=\:\frac{\pi\mathrm{R1}^{\mathrm{2}} \alpha}{\mathrm{360}}\:−\boldsymbol{\mathrm{R}}\mathrm{1}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \boldsymbol{\alpha} \\ $$$$\:\:\boldsymbol{\mathrm{S}}\left(\boldsymbol{\mathrm{AO}}'\boldsymbol{\mathrm{M}}\right)=\frac{\boldsymbol{\pi\mathrm{R}}\mathrm{2}×\left(\mathrm{105}−\alpha\right)}{\mathrm{360}}−\boldsymbol{\mathrm{R}}\mathrm{2}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \left(\mathrm{105}−\alpha\right) \\ $$$$\left(\beta=\mathrm{105}−\alpha\right) \\ $$$$\:\:\:\left(\boldsymbol{{A}}\:\boldsymbol{{Suivre}}\right)........... \\ $$$$ \\ $$$$\bigtriangleup\boldsymbol{\mathrm{AOM}}\:/\boldsymbol{\mathrm{AO}}'\boldsymbol{\mathrm{M}} \\ $$$$\boldsymbol{\mathrm{OM}}^{\mathrm{2}} =\boldsymbol{\mathrm{AO}}^{\mathrm{2}} +\boldsymbol{\mathrm{AM}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{AO}}×\boldsymbol{\mathrm{AM}}\mathrm{cos}\:\boldsymbol{\alpha} \\ $$$$\boldsymbol{\mathrm{R}}\mathrm{1}^{\mathrm{2}} =\boldsymbol{\mathrm{R}}\mathrm{1}^{\mathrm{2}} +\boldsymbol{\mathrm{AM}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{AM}}×\boldsymbol{\mathrm{R}}\mathrm{1cos}\:\boldsymbol{\alpha} \\ $$$$\mathrm{0}=\boldsymbol{\mathrm{AM}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{AM}}×\boldsymbol{\mathrm{R}}\mathrm{1cos}\:\boldsymbol{\alpha}\:\:\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{AM}}=\mathrm{2}\boldsymbol{\mathrm{R}}\mathrm{1cos}\:\boldsymbol{\alpha}\:\:\:\:\left(\boldsymbol{\mathrm{i}}\right) \\ $$$$ \\ $$$$\mathrm{de}\:\mathrm{meme} \\ $$$$\:\boldsymbol{\mathrm{AM}}=\mathrm{2}\boldsymbol{\mathrm{R}}\mathrm{2cos}\:\left(\mathrm{105}−\boldsymbol{\alpha}\right) \\ $$$$\Rightarrow\boldsymbol{\mathrm{R}}\mathrm{1cos}\:\boldsymbol{\alpha}=\boldsymbol{\mathrm{R}}\mathrm{2cos}\:\left(\mathrm{105}−\boldsymbol{\alpha}\right) \\ $$$$\:\:\frac{\mathrm{cos}\:\boldsymbol{\alpha}}{\mathrm{cos}\left(\mathrm{105}−\:\boldsymbol{\alpha}\right)}=\frac{\boldsymbol{\mathrm{R}}\mathrm{2}}{\boldsymbol{\mathrm{R}}\mathrm{1}}=\frac{\mathrm{122}}{\mathrm{107}} \\ $$$$\mathrm{122}\left(\mathrm{cos}\:\mathrm{105cos}\:\alpha+\mathrm{sin}\:\:\mathrm{105sin}\:\alpha\right)=\mathrm{107cos}\:\alpha \\ $$$$\left(\mathrm{122cos}\:\mathrm{105}−\mathrm{107}\right)\mathrm{cos}\:\boldsymbol{\alpha}+\mathrm{122}×\mathrm{sin105sin}\:\boldsymbol{\alpha}\:=\mathrm{0} \\ $$$$\left(\mathrm{107}−\mathrm{122cos}\:\mathrm{105}\right)\mathrm{cos}\:\boldsymbol{\alpha}=\mathrm{122sin}\:\boldsymbol{\alpha} \\ $$$$\Rightarrow\:\:\:\mathrm{tan}\:\boldsymbol{\alpha}=\frac{\mathrm{107}−\mathrm{122cos}\:\mathrm{105}}{\mathrm{122}}=\mathrm{1},\mathrm{135} \\ $$$$\:\:\:\:\:\:\:\:\:\:\measuredangle\boldsymbol{\mathrm{OAM}}\:\:\:=\mathrm{48},\mathrm{6}° \\ $$$$\:\:\:\boldsymbol{\mathrm{AM}}=\mathrm{4},\mathrm{28cos}\:\boldsymbol{\alpha}=\mathrm{2},\mathrm{83} \\ $$$$\Rightarrow\measuredangle\boldsymbol{\mathrm{AOH}}\:\approx\mathrm{90}−\mathrm{48}=\mathrm{42}° \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{S}}\mathrm{1}=\frac{\boldsymbol{\pi\mathrm{R}}^{\mathrm{2}} \mathrm{1}×\mathrm{84}}{\mathrm{360}}−\left(\frac{\mathrm{2},\mathrm{83}}{\mathrm{2}}\right)×\boldsymbol{\mathrm{R}}\mathrm{1cos}\:\mathrm{42} \\ $$$$\boldsymbol{\mathrm{S}}\mathrm{1}=\mathrm{3},\mathrm{357}−\mathrm{2},\mathrm{25}=\mathrm{1},\mathrm{106} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{S}}\mathrm{2}=\frac{\boldsymbol{\pi\mathrm{R}}\mathrm{2}^{\mathrm{2}} ×\mathrm{57}}{\mathrm{360}}−\left(\frac{\mathrm{2},\mathrm{83}}{\mathrm{2}}\right)×\boldsymbol{\mathrm{R}}\mathrm{2cos}\:\mathrm{33} \\ $$$$=\mathrm{2},\mathrm{961}−\mathrm{2},\mathrm{895}=\mathrm{0},\mathrm{066} \\ $$$$ \\ $$$$\:\:\:\:\boldsymbol{\mathrm{Surface}}\:\:\boldsymbol{\mathrm{est}}\:\:\:\mathrm{1},\mathrm{106}+\mathrm{0},\mathrm{066} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{S}}=\:\:\mathrm{1},\mathrm{172} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 05/Oct/23
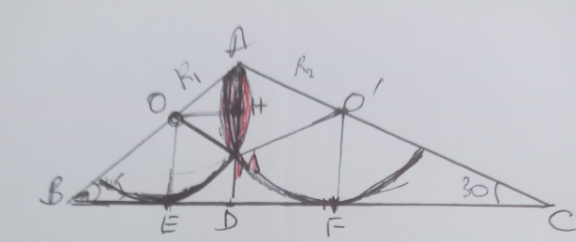
Answered by a.lgnaoui last updated on 06/Oct/23