
Question Number 197821 by mnjuly1970 last updated on 30/Sep/23
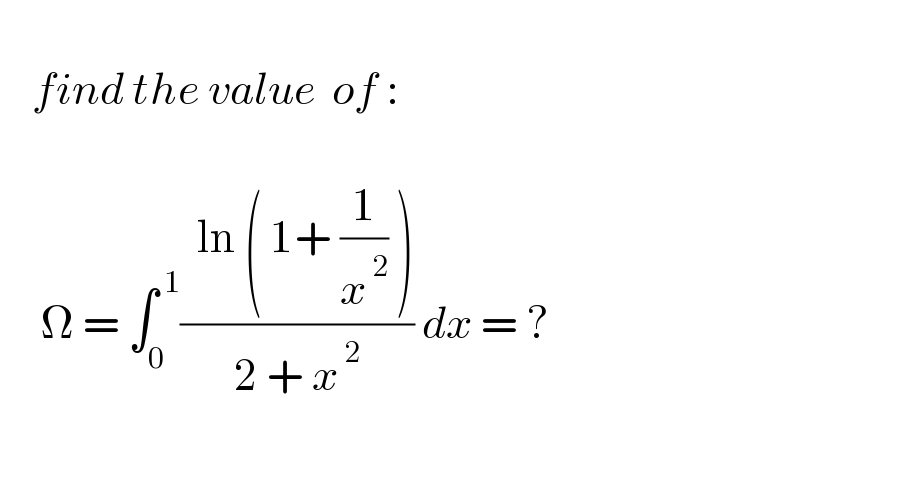
$$ \\ $$$$\:\:\:\:{find}\:{the}\:{value}\:\:{of}\:: \\ $$$$ \\ $$$$\:\:\:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\:\mathrm{ln}\:\left(\:\mathrm{1}+\:\frac{\mathrm{1}}{{x}^{\:\mathrm{2}} }\:\right)}{\mathrm{2}\:+\:{x}^{\:\mathrm{2}} }\:{dx}\:=\:? \\ $$$$ \\ $$
Answered by witcher3 last updated on 05/Oct/23
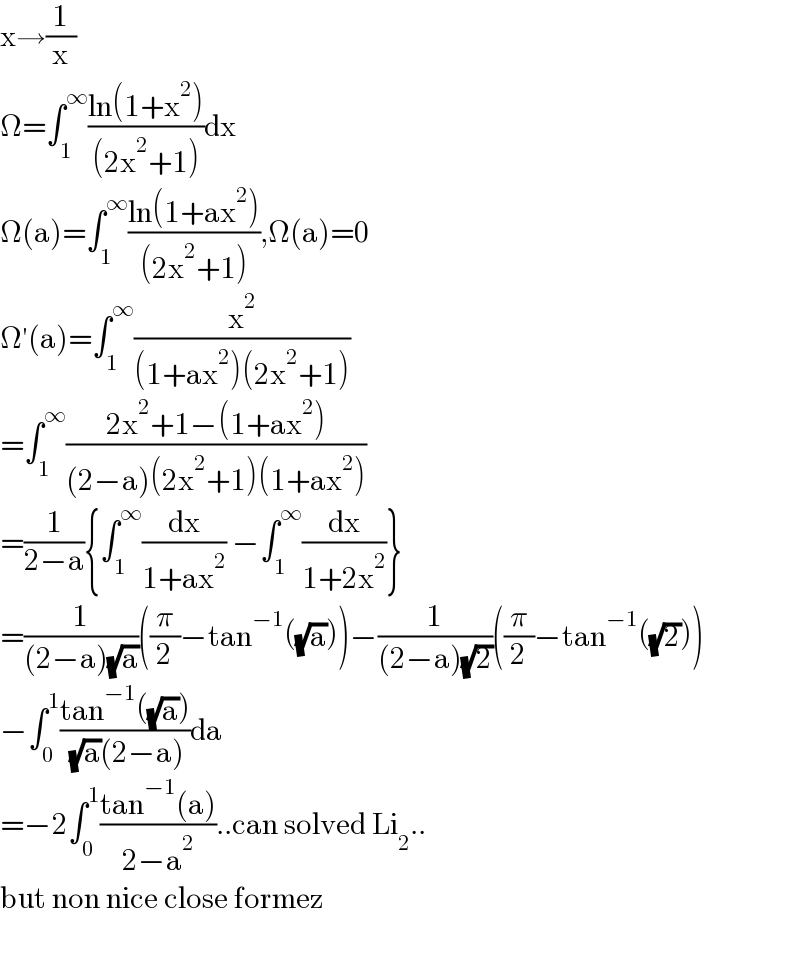
$$\mathrm{x}\rightarrow\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\Omega=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dx} \\ $$$$\Omega\left(\mathrm{a}\right)=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{ax}^{\mathrm{2}} \right)}{\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)},\Omega\left(\mathrm{a}\right)=\mathrm{0} \\ $$$$\Omega'\left(\mathrm{a}\right)=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{ax}^{\mathrm{2}} \right)\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{1}−\left(\mathrm{1}+\mathrm{ax}^{\mathrm{2}} \right)}{\left(\mathrm{2}−\mathrm{a}\right)\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}+\mathrm{ax}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}−\mathrm{a}}\left\{\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{ax}^{\mathrm{2}} }\:−\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{2x}^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{a}\right)\sqrt{\mathrm{a}}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{a}}\right)\right)−\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{a}\right)\sqrt{\mathrm{2}}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}\right)\right) \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{a}}\right)}{\:\sqrt{\mathrm{a}}\left(\mathrm{2}−\mathrm{a}\right)}\mathrm{da} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{a}\right)}{\mathrm{2}−\mathrm{a}^{\mathrm{2}} }..\mathrm{can}\:\mathrm{solved}\:\mathrm{Li}_{\mathrm{2}} .. \\ $$$$\mathrm{but}\:\mathrm{non}\:\mathrm{nice}\:\mathrm{close}\:\mathrm{formez} \\ $$$$ \\ $$
