
Question Number 197795 by cortano12 last updated on 29/Sep/23

Answered by mr W last updated on 29/Sep/23
![(1) x+y=x^2 +y^2 (x−(1/2))^2 +(y−(1/2))^2 =((1/( (√2))))^2 x=(1/2)+(1/( (√2))) cos θ y=(1/2)+(1/( (√2))) sin θ t=x+y=1+sin ((π/4)+θ)=1+sin α ∈[0, 2] x^3 +y^3 =(x+y)^3 −(3/2)(x+y)[(x+y)^2 −x^2 −y^2 ] x^3 +y^3 =(1/2)(x+y)^2 [3−(x+y)] x^3 +y^3 =(1/2)t^2 (3−t) ∈[0, 2] (2) let 2^x =a≠0, 2^y =b≠0 a+b=a^2 +b^2 8^x +8^y =a^3 +b^3 ∈(0, 2]](Q197799.png)
$$\left(\mathrm{1}\right) \\ $$$${x}+{y}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{cos}\:\theta \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{sin}\:\theta \\ $$$${t}={x}+{y}=\mathrm{1}+\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+\theta\right)=\mathrm{1}+\mathrm{sin}\:\alpha\:\in\left[\mathrm{0},\:\mathrm{2}\right] \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\left({x}+{y}\right)^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}}\left({x}+{y}\right)\left[\left({x}+{y}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right] \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\left({x}+{y}\right)^{\mathrm{2}} \left[\mathrm{3}−\left({x}+{y}\right)\right] \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} \left(\mathrm{3}−{t}\right)\:\in\left[\mathrm{0},\:\mathrm{2}\right] \\ $$$$\left(\mathrm{2}\right) \\ $$$${let}\:\mathrm{2}^{{x}} ={a}\neq\mathrm{0},\:\mathrm{2}^{{y}} ={b}\neq\mathrm{0} \\ $$$${a}+{b}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\mathrm{8}^{{x}} +\mathrm{8}^{{y}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} \:\in\left(\mathrm{0},\:\mathrm{2}\right] \\ $$
Answered by Frix last updated on 29/Sep/23
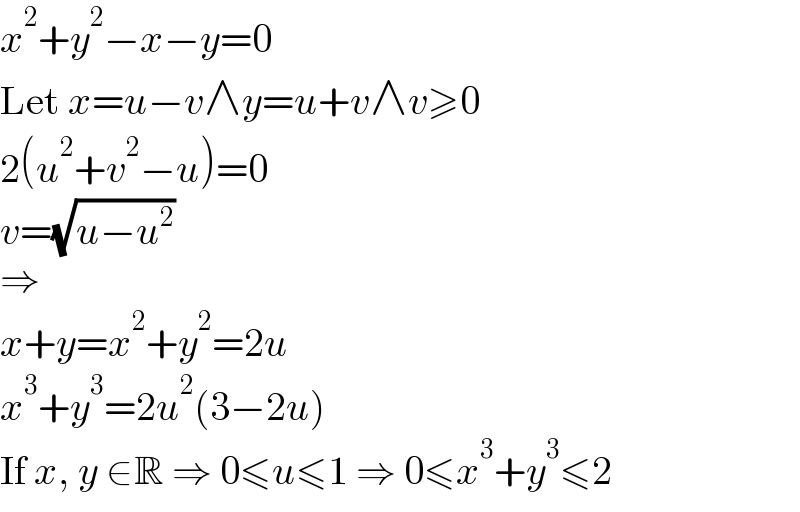
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{x}−{y}=\mathrm{0} \\ $$$$\mathrm{Let}\:{x}={u}−{v}\wedge{y}={u}+{v}\wedge{v}\geqslant\mathrm{0} \\ $$$$\mathrm{2}\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} −{u}\right)=\mathrm{0} \\ $$$${v}=\sqrt{{u}−{u}^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$${x}+{y}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2}{u} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\mathrm{2}{u}^{\mathrm{2}} \left(\mathrm{3}−\mathrm{2}{u}\right) \\ $$$$\mathrm{If}\:{x},\:{y}\:\in\mathbb{R}\:\Rightarrow\:\mathrm{0}\leqslant{u}\leqslant\mathrm{1}\:\Rightarrow\:\mathrm{0}\leqslant{x}^{\mathrm{3}} +{y}^{\mathrm{3}} \leqslant\mathrm{2} \\ $$
