Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 197794 by universe last updated on 28/Sep/23

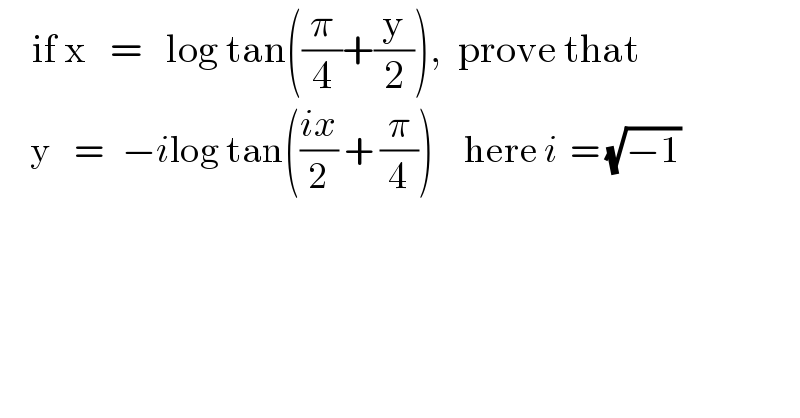
if x = log tan((π/4)+(y/2)), prove that y = −ilog tan(((ix)/2) + (π/4)) here i = (√(−1))

$$\:\:\:\:\mathrm{if}\:\mathrm{x}\:\:\:=\:\:\:\mathrm{log}\:\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}+\frac{\mathrm{y}}{\mathrm{2}}\right),\:\:\mathrm{prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\mathrm{y}\:\:\:\:=\:\:\:−{i}\mathrm{log}\:\mathrm{tan}\left(\frac{{ix}}{\mathrm{2}}\:+\:\frac{\pi}{\mathrm{4}}\right)\:\:\:\:\:\mathrm{here}\:{i}\:\:=\:\sqrt{−\mathrm{1}} \\ $$

Answered by Frix last updated on 29/Sep/23

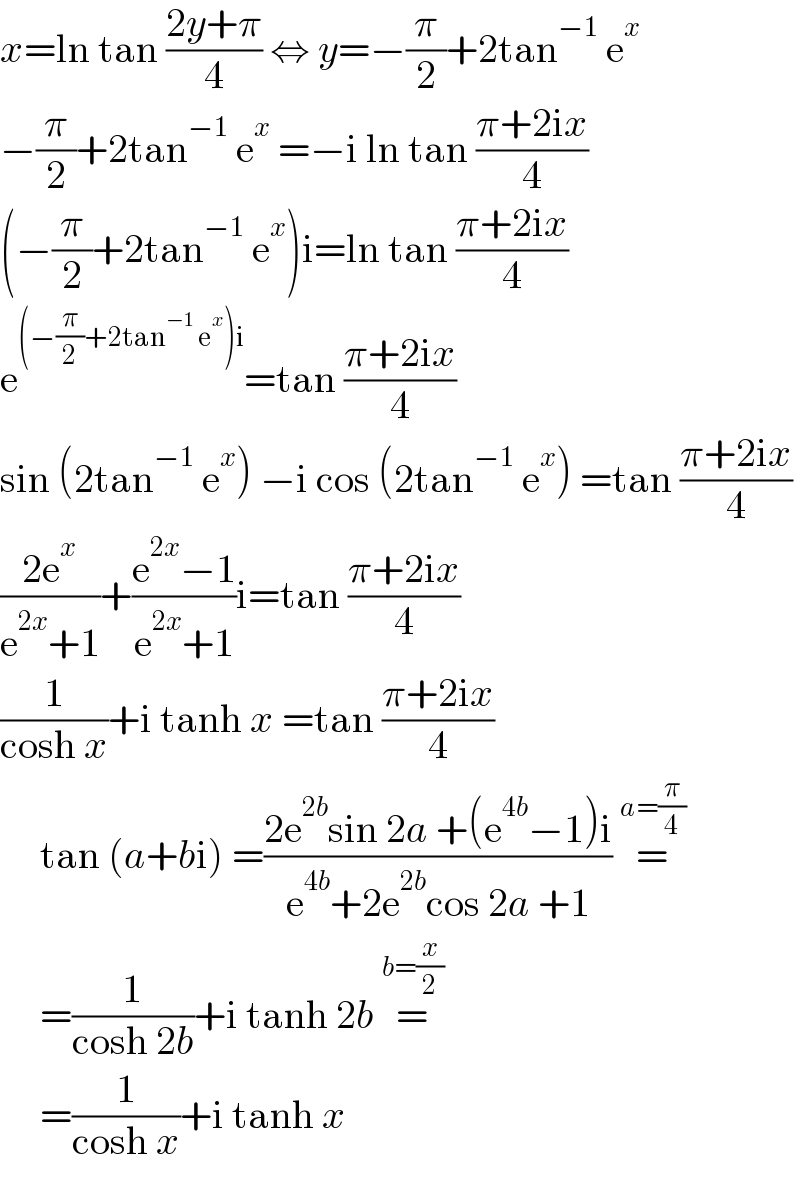
x=ln tan ((2y+π)/4) ⇔ y=−(π/2)+2tan^(−1) e^x −(π/2)+2tan^(−1) e^x =−i ln tan ((π+2ix)/4) (−(π/2)+2tan^(−1) e^x )i=ln tan ((π+2ix)/4) e^((−(π/2)+2tan^(−1) e^x )i) =tan ((π+2ix)/4) sin (2tan^(−1) e^x ) −i cos (2tan^(−1) e^x ) =tan ((π+2ix)/4) ((2e^x )/(e^(2x) +1))+((e^(2x) −1)/(e^(2x) +1))i=tan ((π+2ix)/4) (1/(cosh x))+i tanh x =tan ((π+2ix)/4) tan (a+bi) =((2e^(2b) sin 2a +(e^(4b) −1)i)/(e^(4b) +2e^(2b) cos 2a +1)) =^(a=(π/4)) =(1/(cosh 2b))+i tanh 2b =^(b=(x/2)) =(1/(cosh x))+i tanh x

$${x}=\mathrm{ln}\:\mathrm{tan}\:\frac{\mathrm{2}{y}+\pi}{\mathrm{4}}\:\Leftrightarrow\:{y}=−\frac{\pi}{\mathrm{2}}+\mathrm{2tan}^{−\mathrm{1}} \:\mathrm{e}^{{x}} \\ $$$$−\frac{\pi}{\mathrm{2}}+\mathrm{2tan}^{−\mathrm{1}} \:\mathrm{e}^{{x}} \:=−\mathrm{i}\:\mathrm{ln}\:\mathrm{tan}\:\frac{\pi+\mathrm{2i}{x}}{\mathrm{4}} \\ $$$$\left(−\frac{\pi}{\mathrm{2}}+\mathrm{2tan}^{−\mathrm{1}} \:\mathrm{e}^{{x}} \right)\mathrm{i}=\mathrm{ln}\:\mathrm{tan}\:\frac{\pi+\mathrm{2i}{x}}{\mathrm{4}} \\ $$$$\mathrm{e}^{\left(−\frac{\pi}{\mathrm{2}}+\mathrm{2tan}^{−\mathrm{1}} \:\mathrm{e}^{{x}} \right)\mathrm{i}} =\mathrm{tan}\:\frac{\pi+\mathrm{2i}{x}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\left(\mathrm{2tan}^{−\mathrm{1}} \:\mathrm{e}^{{x}} \right)\:−\mathrm{i}\:\mathrm{cos}\:\left(\mathrm{2tan}^{−\mathrm{1}} \:\mathrm{e}^{{x}} \right)\:=\mathrm{tan}\:\frac{\pi+\mathrm{2i}{x}}{\mathrm{4}} \\ $$$$\frac{\mathrm{2e}^{{x}} }{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{1}}+\frac{\mathrm{e}^{\mathrm{2}{x}} −\mathrm{1}}{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{1}}\mathrm{i}=\mathrm{tan}\:\frac{\pi+\mathrm{2i}{x}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{cosh}\:{x}}+\mathrm{i}\:\mathrm{tanh}\:{x}\:=\mathrm{tan}\:\frac{\pi+\mathrm{2i}{x}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\mathrm{tan}\:\left({a}+{b}\mathrm{i}\right)\:=\frac{\mathrm{2e}^{\mathrm{2}{b}} \mathrm{sin}\:\mathrm{2}{a}\:+\left(\mathrm{e}^{\mathrm{4}{b}} −\mathrm{1}\right)\mathrm{i}}{\mathrm{e}^{\mathrm{4}{b}} +\mathrm{2e}^{\mathrm{2}{b}} \mathrm{cos}\:\mathrm{2}{a}\:+\mathrm{1}}\:\overset{{a}=\frac{\pi}{\mathrm{4}}} {=} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{cosh}\:\mathrm{2}{b}}+\mathrm{i}\:\mathrm{tanh}\:\mathrm{2}{b}\:\overset{{b}=\frac{{x}}{\mathrm{2}}} {=} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{cosh}\:{x}}+\mathrm{i}\:\mathrm{tanh}\:{x} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com