
Question Number 198815 by a.lgnaoui last updated on 24/Oct/23
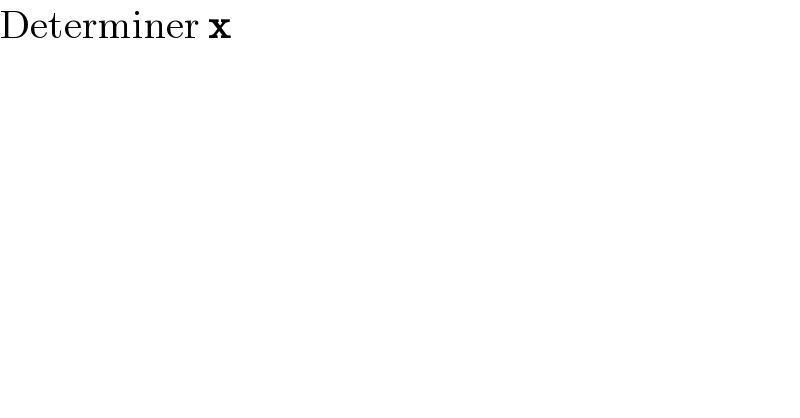
$$\mathrm{Determiner}\:\boldsymbol{\mathrm{x}} \\ $$
Commented by a.lgnaoui last updated on 24/Oct/23
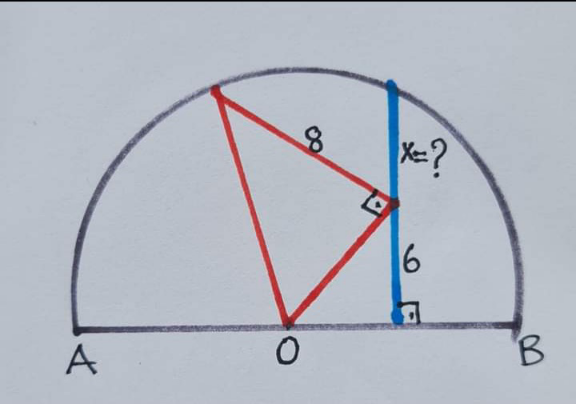
Commented by cherokeesay last updated on 24/Oct/23
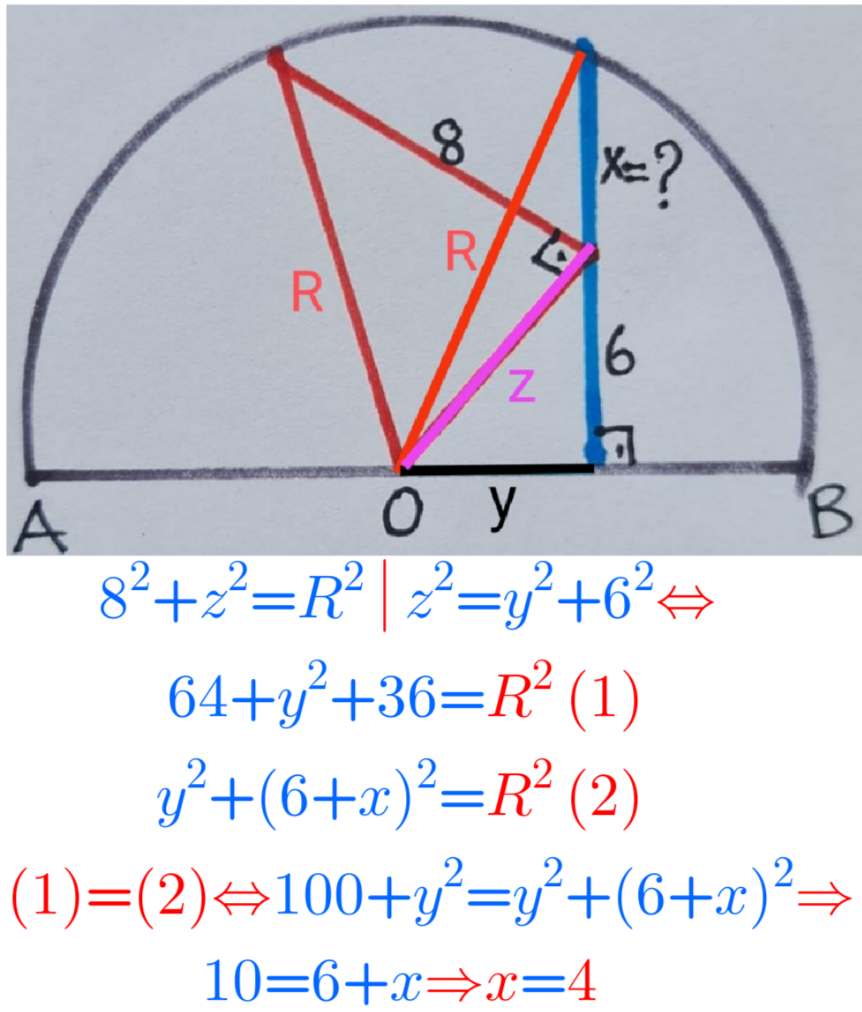
Commented by a.lgnaoui last updated on 24/Oct/23
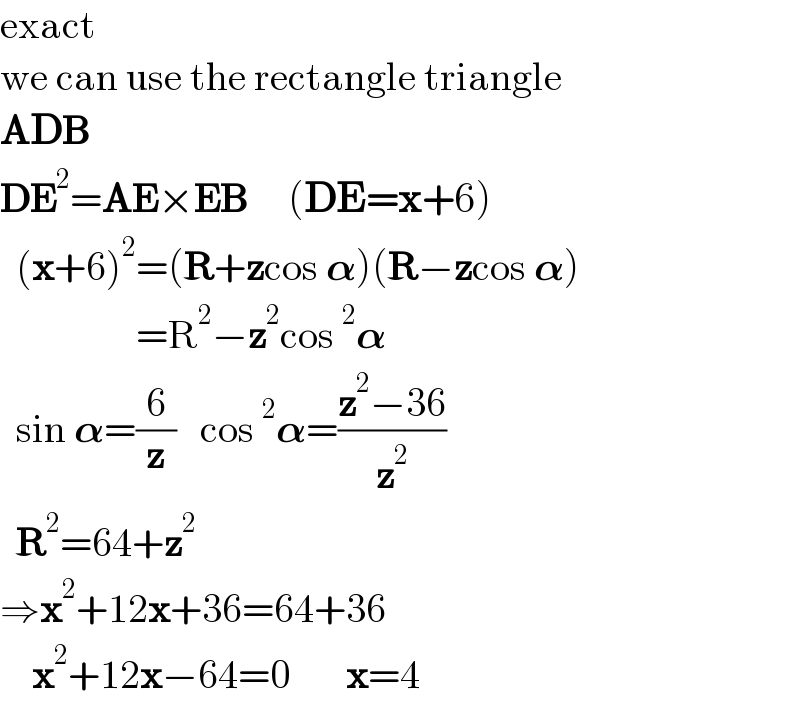
$$\mathrm{exact} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{the}\:\mathrm{rectangle}\:\mathrm{triangle} \\ $$$$\boldsymbol{\mathrm{ADB}} \\ $$$$\boldsymbol{\mathrm{DE}}^{\mathrm{2}} =\boldsymbol{\mathrm{AE}}×\boldsymbol{\mathrm{EB}}\:\:\:\:\:\left(\boldsymbol{\mathrm{DE}}=\boldsymbol{\mathrm{x}}+\mathrm{6}\right) \\ $$$$\:\:\left(\boldsymbol{\mathrm{x}}+\mathrm{6}\right)^{\mathrm{2}} =\left(\boldsymbol{\mathrm{R}}+\boldsymbol{\mathrm{z}}\mathrm{cos}\:\boldsymbol{\alpha}\right)\left(\boldsymbol{\mathrm{R}}−\boldsymbol{\mathrm{z}}\mathrm{cos}\:\boldsymbol{\alpha}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{R}^{\mathrm{2}} −\boldsymbol{\mathrm{z}}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \boldsymbol{\alpha} \\ $$$$\:\:\mathrm{sin}\:\boldsymbol{\alpha}=\frac{\mathrm{6}}{\boldsymbol{\mathrm{z}}}\:\:\:\mathrm{cos}\:^{\mathrm{2}} \boldsymbol{\alpha}=\frac{\boldsymbol{\mathrm{z}}^{\mathrm{2}} −\mathrm{36}}{\boldsymbol{\mathrm{z}}^{\mathrm{2}} } \\ $$$$\:\:\boldsymbol{\mathrm{R}}^{\mathrm{2}} =\mathrm{64}+\boldsymbol{\mathrm{z}}^{\mathrm{2}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{12}\boldsymbol{\mathrm{x}}+\mathrm{36}=\mathrm{64}+\mathrm{36} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{12}\boldsymbol{\mathrm{x}}−\mathrm{64}=\mathrm{0}\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}=\mathrm{4} \\ $$
