
Question Number 19734 by Tinkutara last updated on 15/Aug/17
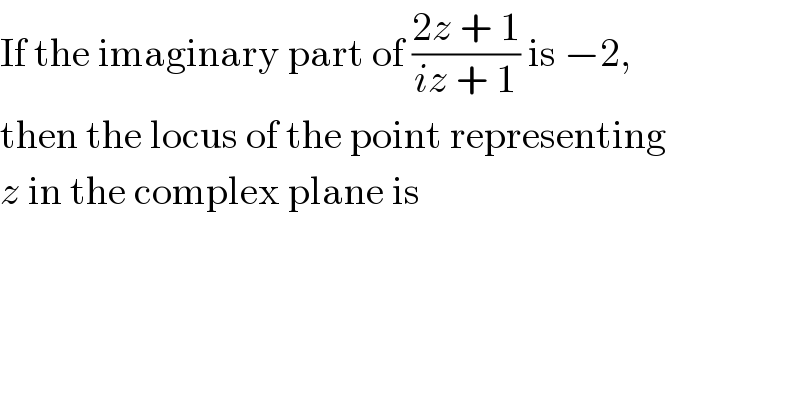
$$\mathrm{If}\:\mathrm{the}\:\mathrm{imaginary}\:\mathrm{part}\:\mathrm{of}\:\frac{\mathrm{2}{z}\:+\:\mathrm{1}}{{iz}\:+\:\mathrm{1}}\:\mathrm{is}\:−\mathrm{2}, \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{the}\:\mathrm{point}\:\mathrm{representing} \\ $$$${z}\:\mathrm{in}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{plane}\:\mathrm{is} \\ $$
Answered by ajfour last updated on 15/Aug/17
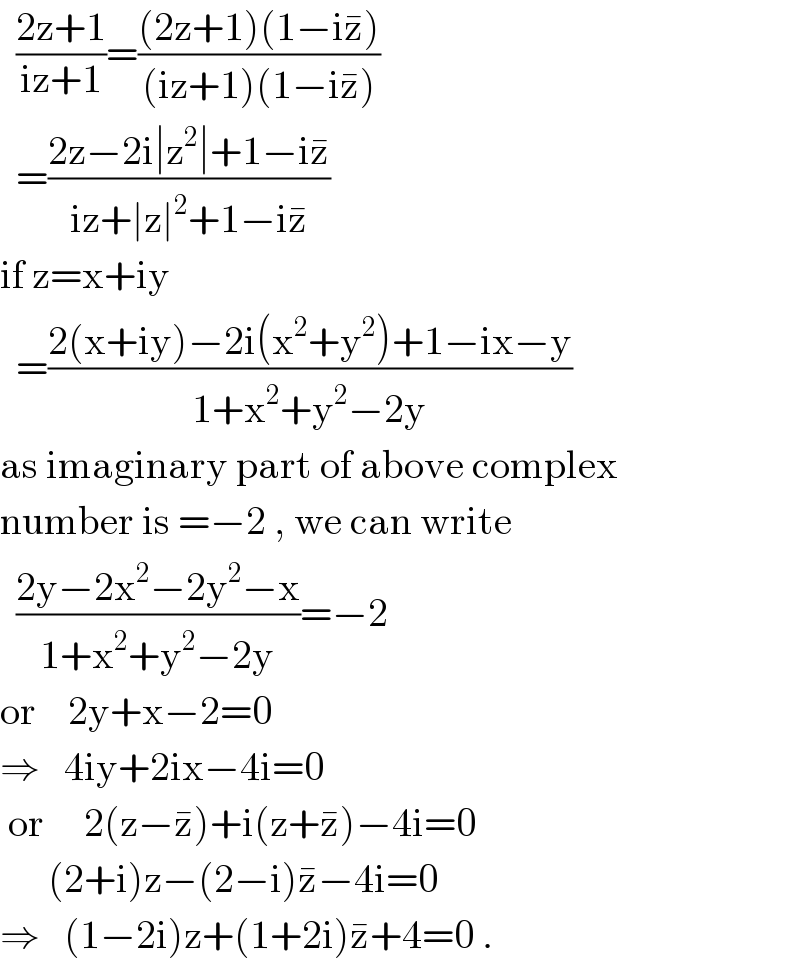
$$\:\:\frac{\mathrm{2z}+\mathrm{1}}{\mathrm{iz}+\mathrm{1}}=\frac{\left(\mathrm{2z}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{i}\bar {\mathrm{z}}\right)}{\left(\mathrm{iz}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{i}\bar {\mathrm{z}}\right)} \\ $$$$\:\:=\frac{\mathrm{2z}−\mathrm{2i}\mid\mathrm{z}^{\mathrm{2}} \mid+\mathrm{1}−\mathrm{i}\bar {\mathrm{z}}}{\mathrm{iz}+\mid\mathrm{z}\mid^{\mathrm{2}} +\mathrm{1}−\mathrm{i}\bar {\mathrm{z}}} \\ $$$$\mathrm{if}\:\mathrm{z}=\mathrm{x}+\mathrm{iy} \\ $$$$\:\:=\frac{\mathrm{2}\left(\mathrm{x}+\mathrm{iy}\right)−\mathrm{2i}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)+\mathrm{1}−\mathrm{ix}−\mathrm{y}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2y}} \\ $$$$\mathrm{as}\:\mathrm{imaginary}\:\mathrm{part}\:\mathrm{of}\:\mathrm{above}\:\mathrm{complex} \\ $$$$\mathrm{number}\:\mathrm{is}\:=−\mathrm{2}\:,\:\mathrm{we}\:\mathrm{can}\:\mathrm{write} \\ $$$$\:\:\frac{\mathrm{2y}−\mathrm{2x}^{\mathrm{2}} −\mathrm{2y}^{\mathrm{2}} −\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2y}}=−\mathrm{2} \\ $$$$\mathrm{or}\:\:\:\:\mathrm{2y}+\mathrm{x}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{4iy}+\mathrm{2ix}−\mathrm{4i}=\mathrm{0} \\ $$$$\:\mathrm{or}\:\:\:\:\:\mathrm{2}\left(\mathrm{z}−\bar {\mathrm{z}}\right)+\mathrm{i}\left(\mathrm{z}+\bar {\mathrm{z}}\right)−\mathrm{4i}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\left(\mathrm{2}+\mathrm{i}\right)\mathrm{z}−\left(\mathrm{2}−\mathrm{i}\right)\bar {\mathrm{z}}−\mathrm{4i}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\left(\mathrm{1}−\mathrm{2i}\right)\mathrm{z}+\left(\mathrm{1}+\mathrm{2i}\right)\bar {\mathrm{z}}+\mathrm{4}=\mathrm{0}\:. \\ $$
Commented by Tinkutara last updated on 15/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
