
Question Number 19704 by Tinkutara last updated on 14/Aug/17
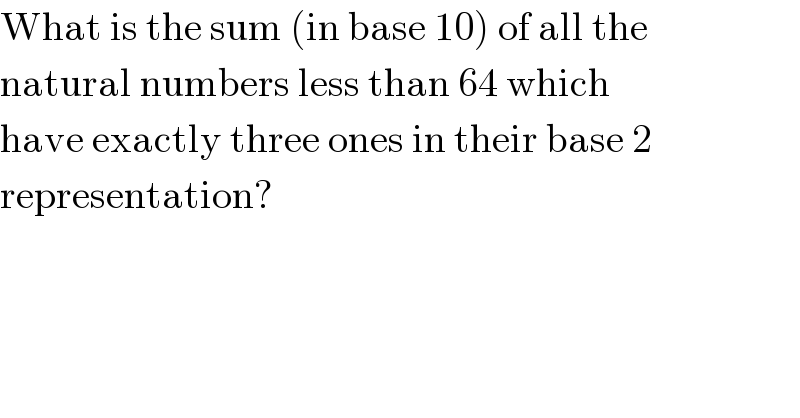
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\left(\mathrm{in}\:\mathrm{base}\:\mathrm{10}\right)\:\mathrm{of}\:\mathrm{all}\:\mathrm{the} \\ $$$$\mathrm{natural}\:\mathrm{numbers}\:\mathrm{less}\:\mathrm{than}\:\mathrm{64}\:\mathrm{which} \\ $$$$\mathrm{have}\:\mathrm{exactly}\:\mathrm{three}\:\mathrm{ones}\:\mathrm{in}\:\mathrm{their}\:\mathrm{base}\:\mathrm{2} \\ $$$$\mathrm{representation}? \\ $$
Answered by mrW1 last updated on 15/Aug/17

$$``\mathrm{1}''\:\mathrm{means}\:\mathrm{1},\:\mathrm{2},\:\mathrm{4},\:\mathrm{8},\:\mathrm{16},\:\mathrm{32}\:\mathrm{from} \\ $$$$\mathrm{right}\:\mathrm{to}\:\mathrm{left}. \\ $$$$\mathrm{with}\:\mathrm{three}\:``\mathrm{1}''\:\mathrm{we}\:\mathrm{can}\:\mathrm{get} \\ $$$$\mathrm{following}\:\mathrm{possible}\:\mathrm{numbers}: \\ $$$$\mathrm{32}+\mathrm{16}+\mathrm{8} \\ $$$$\mathrm{32}+\mathrm{16}+\mathrm{4} \\ $$$$\mathrm{32}+\mathrm{16}+\mathrm{2} \\ $$$$\mathrm{32}+\mathrm{16}+\mathrm{1}\:\:\:\Rightarrow\:\Sigma=\mathrm{4}×\mathrm{32}+\mathrm{5}×\mathrm{16}−\mathrm{1}=\mathrm{207} \\ $$$$\mathrm{32}+\mathrm{8}+\mathrm{4} \\ $$$$\mathrm{32}+\mathrm{8}+\mathrm{2} \\ $$$$\mathrm{32}+\mathrm{8}+\mathrm{1}\:\:\Rightarrow\:\Sigma=\mathrm{3}×\mathrm{32}+\mathrm{4}×\mathrm{8}−\mathrm{1}=\mathrm{127} \\ $$$$\mathrm{32}+\mathrm{4}+\mathrm{2} \\ $$$$\mathrm{32}+\mathrm{4}+\mathrm{1}\:\Rightarrow\:\Sigma=\mathrm{2}×\mathrm{32}+\mathrm{3}×\mathrm{4}−\mathrm{1}=\mathrm{75} \\ $$$$\mathrm{32}+\mathrm{2}+\mathrm{1}\:\Rightarrow\:\mathrm{35} \\ $$$$\mathrm{16}+\mathrm{8}+\mathrm{4} \\ $$$$\mathrm{16}+\mathrm{8}+\mathrm{2} \\ $$$$\mathrm{16}+\mathrm{8}+\mathrm{1}\:\Rightarrow\:\Sigma=\mathrm{3}×\mathrm{16}+\mathrm{4}×\mathrm{8}−\mathrm{1}=\mathrm{79} \\ $$$$\mathrm{16}+\mathrm{4}+\mathrm{2} \\ $$$$\mathrm{16}+\mathrm{4}+\mathrm{1}\:\Rightarrow\:\Sigma=\mathrm{2}×\mathrm{16}+\mathrm{3}×\mathrm{4}−\mathrm{1}=\mathrm{43} \\ $$$$\mathrm{16}+\mathrm{2}+\mathrm{1}\:\Rightarrow\:\mathrm{19} \\ $$$$\mathrm{8}+\mathrm{4}+\mathrm{2} \\ $$$$\mathrm{8}+\mathrm{4}+\mathrm{1}\:\Rightarrow\:\Sigma=\mathrm{2}×\mathrm{8}+\mathrm{3}×\mathrm{4}−\mathrm{1}=\mathrm{27} \\ $$$$\mathrm{8}+\mathrm{2}+\mathrm{1}\:\Rightarrow\mathrm{11} \\ $$$$\mathrm{4}+\mathrm{2}+\mathrm{1}\:\Rightarrow\:\mathrm{7} \\ $$$$ \\ $$$$\Sigma=\mathrm{207}+\mathrm{127}+\mathrm{75}+\mathrm{35}+\mathrm{79}+\mathrm{43}+\mathrm{19}+\mathrm{27}+\mathrm{11}+\mathrm{7} \\ $$$$=\mathrm{630} \\ $$
Commented by Tinkutara last updated on 15/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by mrW1 last updated on 16/Aug/17
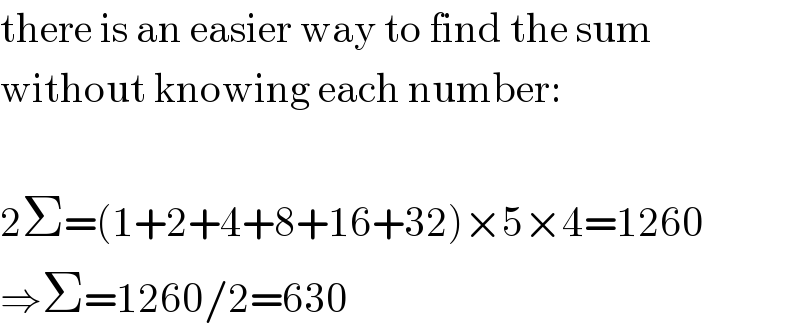
$$\mathrm{there}\:\mathrm{is}\:\mathrm{an}\:\mathrm{easier}\:\mathrm{way}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{sum}\: \\ $$$$\mathrm{without}\:\mathrm{knowing}\:\mathrm{each}\:\mathrm{number}: \\ $$$$ \\ $$$$\mathrm{2}\Sigma=\left(\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{8}+\mathrm{16}+\mathrm{32}\right)×\mathrm{5}×\mathrm{4}=\mathrm{1260} \\ $$$$\Rightarrow\Sigma=\mathrm{1260}/\mathrm{2}=\mathrm{630} \\ $$
Commented by ajfour last updated on 16/Aug/17
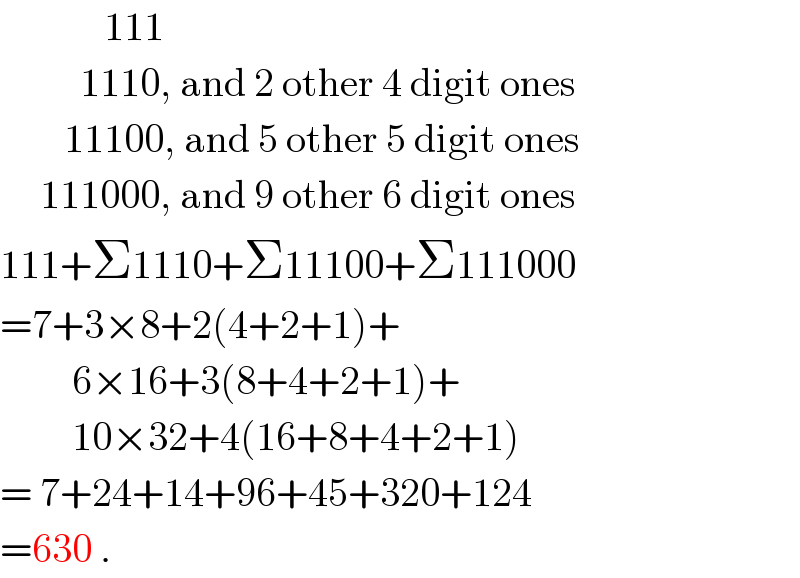
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{111} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{1110},\:\mathrm{and}\:\mathrm{2}\:\mathrm{other}\:\mathrm{4}\:\mathrm{digit}\:\mathrm{ones} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{11100},\:\mathrm{and}\:\mathrm{5}\:\mathrm{other}\:\mathrm{5}\:\mathrm{digit}\:\mathrm{ones} \\ $$$$\:\:\:\:\:\mathrm{111000},\:\mathrm{and}\:\mathrm{9}\:\mathrm{other}\:\mathrm{6}\:\mathrm{digit}\:\mathrm{ones} \\ $$$$\mathrm{111}+\Sigma\mathrm{1110}+\Sigma\mathrm{11100}+\Sigma\mathrm{111000} \\ $$$$=\mathrm{7}+\mathrm{3}×\mathrm{8}+\mathrm{2}\left(\mathrm{4}+\mathrm{2}+\mathrm{1}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{6}×\mathrm{16}+\mathrm{3}\left(\mathrm{8}+\mathrm{4}+\mathrm{2}+\mathrm{1}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{10}×\mathrm{32}+\mathrm{4}\left(\mathrm{16}+\mathrm{8}+\mathrm{4}+\mathrm{2}+\mathrm{1}\right) \\ $$$$=\:\mathrm{7}+\mathrm{24}+\mathrm{14}+\mathrm{96}+\mathrm{45}+\mathrm{320}+\mathrm{124} \\ $$$$=\mathrm{630}\:. \\ $$
Commented by Tinkutara last updated on 16/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{both}\:\mathrm{mrW1}\:\mathrm{and}\:\mathrm{ajfour}. \\ $$
