
Question Number 196929 by Amidip last updated on 03/Sep/23

Answered by som(math1967) last updated on 03/Sep/23
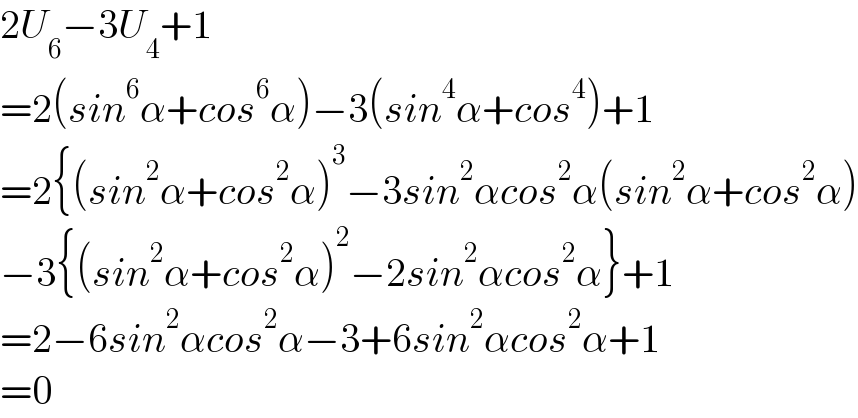
$$\mathrm{2}{U}_{\mathrm{6}} −\mathrm{3}{U}_{\mathrm{4}} +\mathrm{1} \\ $$$$=\mathrm{2}\left({sin}^{\mathrm{6}} \alpha+{cos}^{\mathrm{6}} \alpha\right)−\mathrm{3}\left({sin}^{\mathrm{4}} \alpha+{cos}^{\mathrm{4}} \right)+\mathrm{1} \\ $$$$=\mathrm{2}\left\{\left({sin}^{\mathrm{2}} \alpha+{cos}^{\mathrm{2}} \alpha\right)^{\mathrm{3}} −\mathrm{3}{sin}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \alpha\left({sin}^{\mathrm{2}} \alpha+{cos}^{\mathrm{2}} \alpha\right)\right. \\ $$$$−\mathrm{3}\left\{\left({sin}^{\mathrm{2}} \alpha+{cos}^{\mathrm{2}} \alpha\right)^{\mathrm{2}} −\mathrm{2}{sin}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \alpha\right\}+\mathrm{1} \\ $$$$=\mathrm{2}−\mathrm{6}{sin}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \alpha−\mathrm{3}+\mathrm{6}{sin}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \alpha+\mathrm{1} \\ $$$$=\mathrm{0} \\ $$
