
Question Number 196917 by peter frank last updated on 03/Sep/23

Answered by MM42 last updated on 03/Sep/23

$$\:\:\frac{\mid{PA}\mid}{\mid{PB}\mid}\:=\:\mathrm{3}\:\:\checkmark \\ $$
Commented by peter frank last updated on 03/Sep/23

$$\mathrm{how} \\ $$
Commented by MM42 last updated on 03/Sep/23
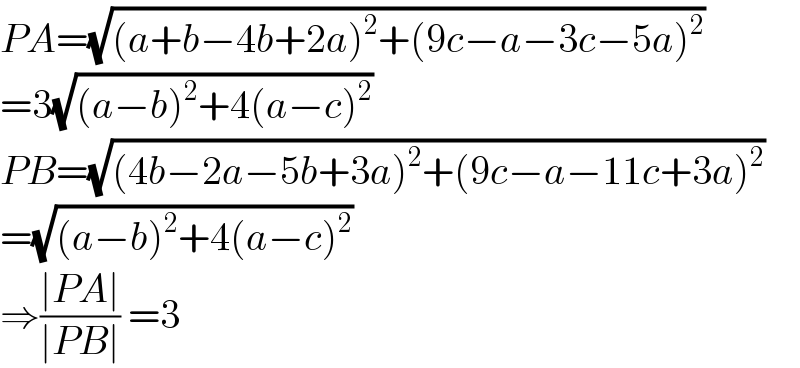
$${PA}=\sqrt{\left({a}+{b}−\mathrm{4}{b}+\mathrm{2}{a}\right)^{\mathrm{2}} +\left(\mathrm{9}{c}−{a}−\mathrm{3}{c}−\mathrm{5}{a}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{3}\sqrt{\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{4}\left({a}−{c}\right)^{\mathrm{2}} } \\ $$$${PB}=\sqrt{\left(\mathrm{4}{b}−\mathrm{2}{a}−\mathrm{5}{b}+\mathrm{3}{a}\right)^{\mathrm{2}} +\left(\mathrm{9}{c}−{a}−\mathrm{11}{c}+\mathrm{3}{a}\right)^{\mathrm{2}} } \\ $$$$=\sqrt{\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{4}\left({a}−{c}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mid{PA}\mid}{\mid{PB}\mid}\:=\mathrm{3} \\ $$
Commented by peter frank last updated on 05/Sep/23

$$\mathrm{thank}\:\mathrm{you}. \\ $$
Answered by som(math1967) last updated on 03/Sep/23
![let PA:PB=m:n ((m(5b−3a)+n(a+b))/(m+n))=4b−2a ⇒m(5b−3a)−m(4b−2a) =n(4b−2a)−n(a+b) ⇒m(b−a)=n×3(b−a) ⇒m:n=3:1 [when a≠b]](Q196923.png)
$${let}\:{PA}:{PB}={m}:{n} \\ $$$$\frac{{m}\left(\mathrm{5}{b}−\mathrm{3}{a}\right)+{n}\left({a}+{b}\right)}{{m}+{n}}=\mathrm{4}{b}−\mathrm{2}{a} \\ $$$$\Rightarrow{m}\left(\mathrm{5}{b}−\mathrm{3}{a}\right)−{m}\left(\mathrm{4}{b}−\mathrm{2}{a}\right) \\ $$$$\:\:\:\:\:\:\:={n}\left(\mathrm{4}{b}−\mathrm{2}{a}\right)−{n}\left({a}+{b}\right) \\ $$$$\Rightarrow{m}\left({b}−{a}\right)={n}×\mathrm{3}\left({b}−{a}\right) \\ $$$$\Rightarrow{m}:{n}=\mathrm{3}:\mathrm{1}\:\:\:\left[{when}\:{a}\neq{b}\right] \\ $$
Commented by JDamian last updated on 03/Sep/23
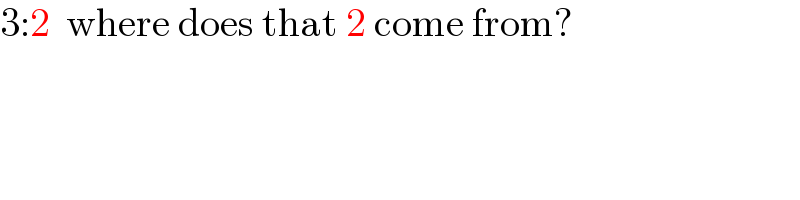
$$\mathrm{3}:\mathrm{2}\:\:\mathrm{where}\:\mathrm{does}\:\mathrm{that}\:\mathrm{2}\:\mathrm{come}\:\mathrm{from}? \\ $$
Commented by som(math1967) last updated on 03/Sep/23

$${sorry}\:{typo} \\ $$
Answered by Nimnim111118 last updated on 05/Sep/23
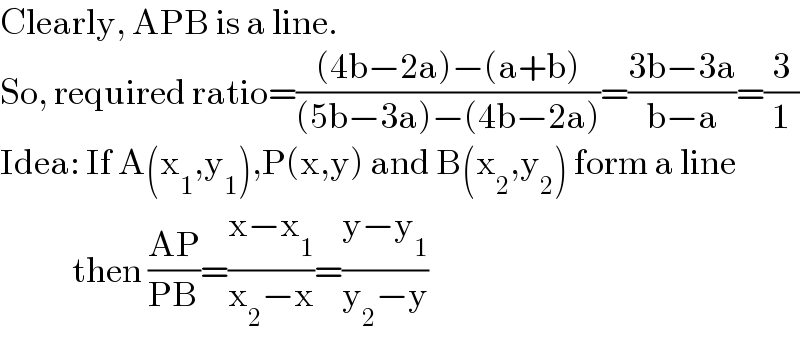
$$\mathrm{Clearly},\:\mathrm{APB}\:\mathrm{is}\:\mathrm{a}\:\mathrm{line}. \\ $$$$\mathrm{So},\:\mathrm{required}\:\mathrm{ratio}=\frac{\left(\mathrm{4b}−\mathrm{2a}\right)−\left(\mathrm{a}+\mathrm{b}\right)}{\left(\mathrm{5b}−\mathrm{3a}\right)−\left(\mathrm{4b}−\mathrm{2a}\right)}=\frac{\mathrm{3b}−\mathrm{3a}}{\mathrm{b}−\mathrm{a}}=\frac{\mathrm{3}}{\mathrm{1}} \\ $$$$\mathrm{Idea}:\:\mathrm{If}\:\mathrm{A}\left(\mathrm{x}_{\mathrm{1}} ,\mathrm{y}_{\mathrm{1}} \right),\mathrm{P}\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{and}\:\mathrm{B}\left(\mathrm{x}_{\mathrm{2}} ,\mathrm{y}_{\mathrm{2}} \right)\:\mathrm{form}\:\mathrm{a}\:\mathrm{line} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{then}\:\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{\mathrm{x}−\mathrm{x}_{\mathrm{1}} }{\mathrm{x}_{\mathrm{2}} −\mathrm{x}}=\frac{\mathrm{y}−\mathrm{y}_{\mathrm{1}} }{\mathrm{y}_{\mathrm{2}} −\mathrm{y}} \\ $$
Commented by peter frank last updated on 05/Sep/23

$$\mathrm{thank}\:\mathrm{you} \\ $$
