
Question Number 196883 by Amidip last updated on 02/Sep/23
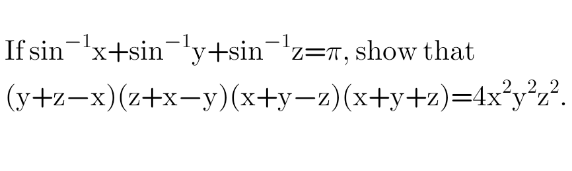
Answered by som(math1967) last updated on 02/Sep/23
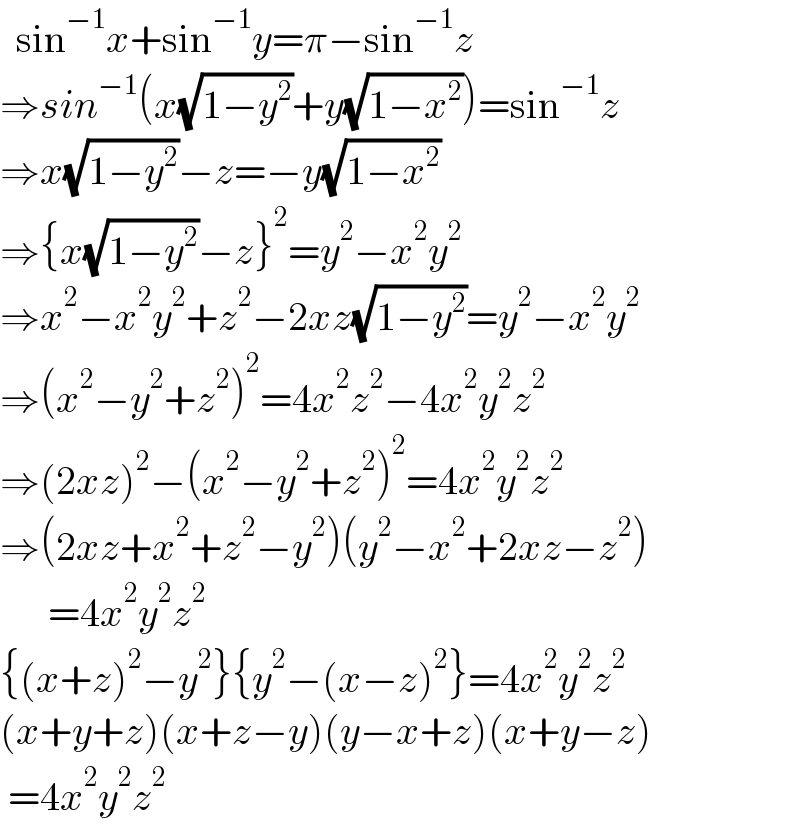
$$\:\:\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} {y}=\pi−\mathrm{sin}^{−\mathrm{1}} {z} \\ $$$$\Rightarrow{sin}^{−\mathrm{1}} \left({x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }+{y}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)=\mathrm{sin}^{−\mathrm{1}} {z} \\ $$$$\Rightarrow{x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }−{z}=−{y}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\left\{{x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }−{z}\right\}^{\mathrm{2}} ={y}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{z}^{\mathrm{2}} −\mathrm{2}{xz}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }={y}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} {z}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} {z}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{2}{xz}\right)^{\mathrm{2}} −\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} {z}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{2}{xz}+{x}^{\mathrm{2}} +{z}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\left({y}^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{2}{xz}−{z}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:=\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} {z}^{\mathrm{2}} \\ $$$$\left\{\left({x}+{z}\right)^{\mathrm{2}} −{y}^{\mathrm{2}} \right\}\left\{{y}^{\mathrm{2}} −\left({x}−{z}\right)^{\mathrm{2}} \right\}=\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} {z}^{\mathrm{2}} \\ $$$$\left({x}+{y}+{z}\right)\left({x}+{z}−{y}\right)\left({y}−{x}+{z}\right)\left({x}+{y}−{z}\right) \\ $$$$\:=\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} {z}^{\mathrm{2}} \\ $$
