
Question Number 19688 by Tinkutara last updated on 14/Aug/17
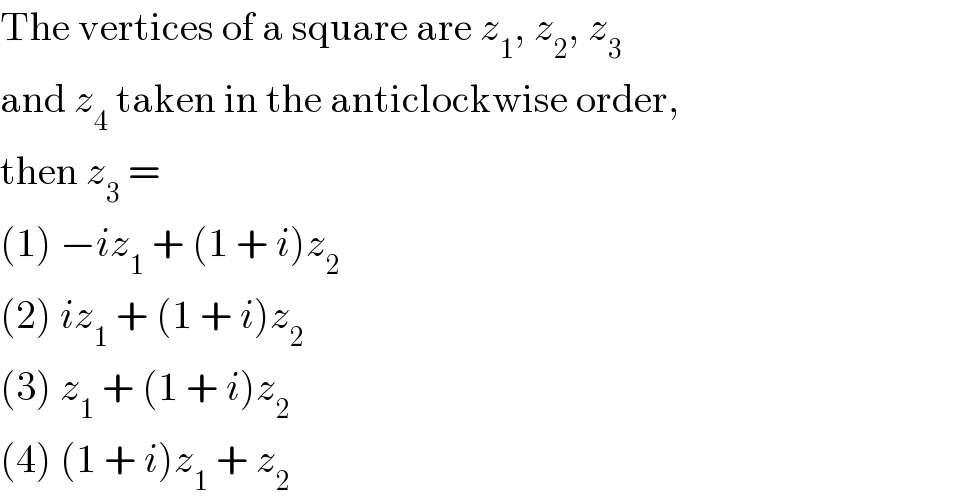
$$\mathrm{The}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{a}\:\mathrm{square}\:\mathrm{are}\:{z}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} ,\:{z}_{\mathrm{3}} \\ $$$$\mathrm{and}\:{z}_{\mathrm{4}} \:\mathrm{taken}\:\mathrm{in}\:\mathrm{the}\:\mathrm{anticlockwise}\:\mathrm{order}, \\ $$$$\mathrm{then}\:{z}_{\mathrm{3}} \:= \\ $$$$\left(\mathrm{1}\right)\:−{iz}_{\mathrm{1}} \:+\:\left(\mathrm{1}\:+\:{i}\right){z}_{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:{iz}_{\mathrm{1}} \:+\:\left(\mathrm{1}\:+\:{i}\right){z}_{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:{z}_{\mathrm{1}} \:+\:\left(\mathrm{1}\:+\:{i}\right){z}_{\mathrm{2}} \\ $$$$\left(\mathrm{4}\right)\:\left(\mathrm{1}\:+\:{i}\right){z}_{\mathrm{1}} \:+\:{z}_{\mathrm{2}} \\ $$
Answered by ajfour last updated on 14/Aug/17
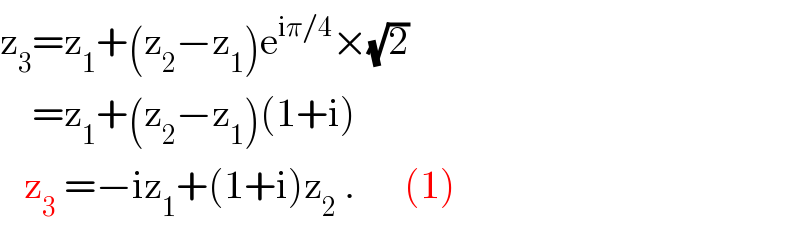
$$\mathrm{z}_{\mathrm{3}} =\mathrm{z}_{\mathrm{1}} +\left(\mathrm{z}_{\mathrm{2}} −\mathrm{z}_{\mathrm{1}} \right)\mathrm{e}^{\mathrm{i}\pi/\mathrm{4}} ×\sqrt{\mathrm{2}}\: \\ $$$$\:\:\:\:=\mathrm{z}_{\mathrm{1}} +\left(\mathrm{z}_{\mathrm{2}} −\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{1}+\mathrm{i}\right) \\ $$$$\:\:\:\mathrm{z}_{\mathrm{3}} \:=−\mathrm{iz}_{\mathrm{1}} +\left(\mathrm{1}+\mathrm{i}\right)\mathrm{z}_{\mathrm{2}} \:.\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$
Commented by Tinkutara last updated on 15/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
