
Question Number 196757 by MrGHK last updated on 31/Aug/23

Answered by qaz last updated on 31/Aug/23
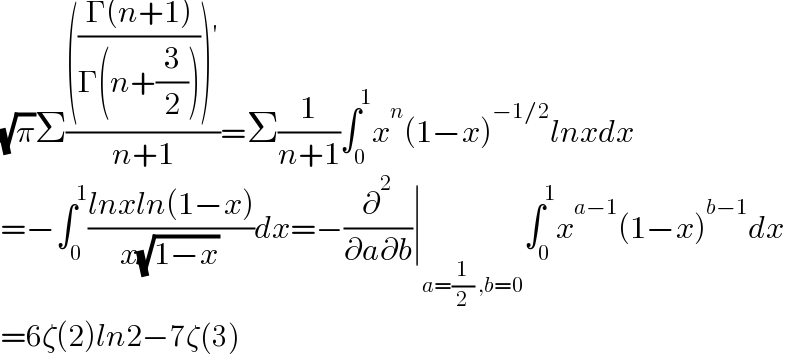
$$\sqrt{\pi}\Sigma\frac{\left(\frac{\Gamma\left({n}+\mathrm{1}\right)}{\Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\right)'}{{n}+\mathrm{1}}=\Sigma\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left(\mathrm{1}−{x}\right)^{−\mathrm{1}/\mathrm{2}} {lnxdx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{lnxln}\left(\mathrm{1}−{x}\right)}{{x}\sqrt{\mathrm{1}−{x}}}{dx}=−\frac{\partial^{\mathrm{2}} }{\partial{a}\partial{b}}\mid_{{a}=\frac{\mathrm{1}}{\mathrm{2}}\:,{b}=\mathrm{0}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{b}−\mathrm{1}} {dx} \\ $$$$=\mathrm{6}\zeta\left(\mathrm{2}\right){ln}\mathrm{2}−\mathrm{7}\zeta\left(\mathrm{3}\right) \\ $$
Commented by MrGHK last updated on 31/Aug/23
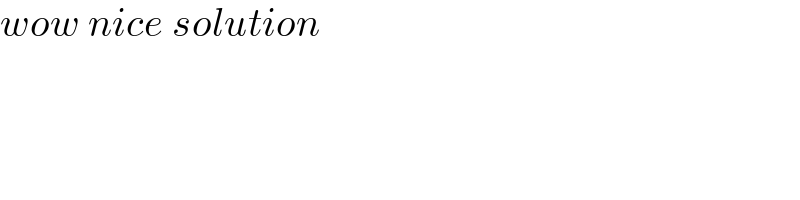
$${wow}\:{nice}\:{solution} \\ $$
Commented by deleted41 last updated on 01/Sep/23
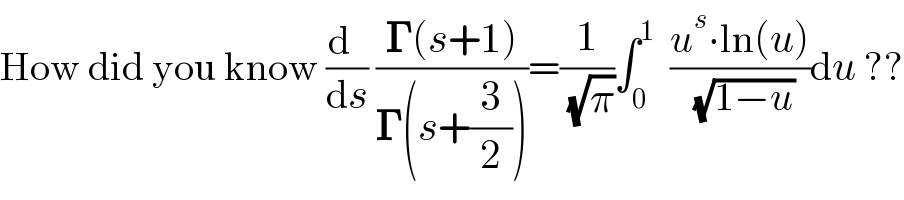
$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{know}\:\frac{\mathrm{d}\:\:}{\mathrm{d}{s}}\:\frac{\boldsymbol{\Gamma}\left({s}+\mathrm{1}\right)}{\boldsymbol{\Gamma}\left({s}+\frac{\mathrm{3}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{u}^{{s}} \centerdot\mathrm{ln}\left({u}\right)}{\:\sqrt{\mathrm{1}−{u}}}\mathrm{d}{u}\:?? \\ $$
